Mesure du temps et navigation

• Accueil
• À ne pas manquer
• Calendriers Saga
• Études thématiques
• Mesure du temps et navigation

Avertissement

Dans cette page, nous allons essayer de comprendre pourquoi il était nécessaire de posséder des instruments de mesure du temps fiables et précis pour faire le point en mer dans les siècles passés.

N'étant en aucun cas un spécialiste de la chose, il n'est pas dans mes intentions de donner ici une quelconque leçon de navigation.

Les coordonnées terrestres

Nous allons rapidement nous remettre en mémoire quelques notions simples.

Pour définir avec précision un point sur la surface de la Terre nous utilisons le système des latitudes et longitudes.

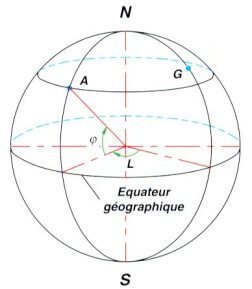
Les latitudes ont pour référence le plan de l'équateur qui est perpendiculaire à l'axe des pôles N-S

Les longitudes ont pour référence le plan méridien qui est défini par le lieu A et l'axe des pôles N-S

Le méridien est le cercle déterminé à la surface de la Terre par le plan méridien. En 1884, c'est la méridien qui passe par l'observatoire de Greenwich (G) comme méridien d'origine.

La longitude (L) est l'angle que fait le méridien local avec celui de Greenwich. Il est mesuré en degrés et minutes et on ajoute si le lieu considéré est à l'est (E) ou à l'ouest (W) de Greenwich.

La latitude d'un lieu est sa distance angulaire avec l'équateur mesurée en degrés et minutes. On ajoute si on se trouve au nord (N) ou au sud (S) de l'équateur.

Par exemple, les coordonnées de Paris sont 48° 52' N (latitude) et 02° 20 E (longitude)

Mesurer la latitude

Nous allons commencer par deux petites expériences.

1) A l'aide d'un logiciel d'astronomie (en l'occurrence le très bon freeware Winstars de Franck Richard qu'on peut trouver ici et qui va nous permettre d'afficher la hauteur des étoiles), regardons la hauteur de l'étoile polaire dans deux villes (à des heures et dates identiques) ayant la même latitude.

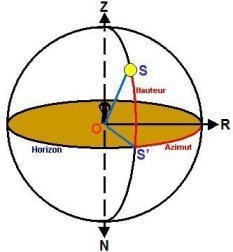
Souvenons nous que le point d'origine des hauteurs (ou altitude) est fixé sur l'horizon local, puis compté de 0° à 90° en partant de l'horizon vers le zénith. Donc nous avons 0° à l'horizon, et 90° au dessus de notre tête (au zénith). La hauteur est donc sur l'image l'angle SOS.

Comment se présente le ciel nocturne dans ces deux villes ?

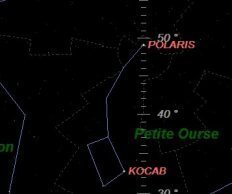
À Brest (France) 48° 23' N 4° 30' W la hauteur de l'étoile polaire (Polaris) est d'environ 49°

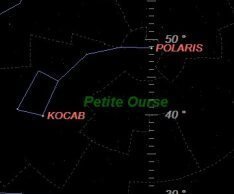
À Port Rexton (Labrador - Canada) 48° 23' N 53° 21' W la hauteur de l'étoile polaire (Polaris) est d'environ 49°

2) A l'aide du même logiciel, regardons la hauteur de l'étoile polaire pour deux villes de même longitude mais de latitudes différentes.

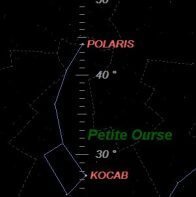
À Marseille (France) 43° 18 N 5° 22 E la hauteur de l'étoile polaire est d'environ 44 °

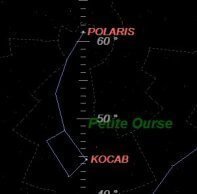
À Bergen (Norvège) 60 ° 23 N 5° 22 E la hauteur de l'étoile polaire est d'environ 61 °

Que pouvons-nous conclure de ces deux observations simples ?

D'une part que la hauteur de l'Étoile polaire est la même à des longitudes différentes et à la même latitude. D'autre part qu'à longitude égale, la hauteur de l'Étoile polaire augmente en même temps que la latitude.

C'est exactement à ces conclusions qu'arrivèrent les premiers navigateurs dès l'antiquité. Ils savaient qu'un degré d'altitude de l'Étoile polaire équivalait à peu près à 20 lieues (80 kilomètres de distance nord-sud) et que la précision était d'environ 30 kilomètres.

Comment expliquer ces observations ?

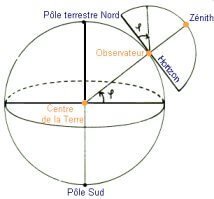
Tout simplement par le fait qu'en visant l'Étoile polaire et en mesurant l'angle qu'elle forme par rapport à notre horizon, c'est comme si nous mesurions, du centre de la Terre, l'angle formé entre la ligne centre-pôle nord et l'équateur.

Du coup, en mesurant la hauteur de l'Étoile polaire, nous obtenons... la latitude... ou presque.

Presque, parce que l'Étoile polaire n'est pas dans le strict prolongement de l'axe nord-sud de la Terre.

Mais comme viser l'horizon la nuit n'est pas des plus facile et, surtout, parce que dès qu'on passe l'équateur vers le sud l'Étoile polaire n'est plus visible et n'a pas d'équivalent au sud, les navigateurs se servirent du Soleil comme astre visé à la place de l'Étoile polaire.

Ce fut quand même au prix d'une difficulté supplémentaire parce que la trajectoire annuelle apparente du Soleil autour de la Terre n'est pas parallèle au plan de l'équateur (voir page astronomie) et varie au cours des saisons ce qui a pour conséquence de faire varier sa hauteur au fil de l'année pour la même latitude. Cette variation est connue sous le nom de déclinaison.

Dès le XIII ème siècle des tables de déclinaisons avaient été établies et l'arrivée de l'imprimerie en 1455 favorisa leur diffusion.

Quant aux instruments de mesure d'altitude, ils furent nombreux et évoluèrent au cours des siècles (astrolobe, nocturlabe, octant, quadrant, arbalète ou arbalestrille, etc.).

Nous n'allons pas décrire ces instruments parce que ce n'est pas notre propos qui est le calcul de la longitude.

Mesurer la longitude

Mesurer la longitude est un problème autrement plus délicat que celui de la latitude. Et pourtant, il est on ne peut plus simple dans la formulation des solutions.

La Terre tourne sur son axe. Ce qui fait que, sur un même parallèle, on voit le même ciel en ce qui concerne le Soleil, la Terre ou les étoiles. La seule différence est qu'on ne le voit pas au même moment.

Alors, les solutions sont simples :

• Comparer l'heure d'observation d'un phénomène céleste en un lieu de longitude de référence avec l'heure locale d'observation du même phénomène dans l'autre lieu.
  Cette méthode oblige à dresser des éphémérides de phénomènes célestes. C'est du ressort de l'astronomie.
• De conserver l'heure du lieu d'origine et de la comparer à l'heure locale de l'autre lieu.
  Cette dernière méthode est du ressort des instruments de mesure du temps et nous concerne particulièrement sur cette page.

La principale difficulté de cette seconde méthode est de construire des instruments de mesure d'une extrême précision. En effet, la Terre tourne de 360 degrés en 24 heures. Sur l'équateur, une heure équivaut à 15 degrés soit 1 666 km. Et une erreur d'une minute (1/60 de degré), c'est une erreur de 27 766 mètres.

Qui plus est, non seulement les instruments doivent être extrêmement précis mais doivent l'être en plus dans des conditions difficiles (humidité, chaleur, froid, instabilité...) qui sont les conséquences de la navigation.

Les difficultés ajoutées de ces deux solutions font que Voltaire parle de « l’impossible problème des longitudes », que Newton est sceptique et que la gueguerre qui va naître entre partisans des deux solutions (astronomique et horlogère) ne va pas arranger les choses.

Et pourtant, dès le XVI ème siècle, il fallait bien trouver une solution à ce grand défi que représentait la longitude parce que...

• Parce que le calcul de la longitude ne concernait pas seulement la navigation mais aussi la cartographie. À quoi bon savoir où on est en mer si on ne sait pas exactement où est la terre la plus proche.
• Parce que les longues expéditions maritimes vers les Indes et le Nouveau Monde se multiplièrent dès le XVI ème siècle avec les profits fabuleux réalisés sur les marchandises et les salaires mirobolants encaissés par les capitaines et les matelots.
• Parce que l'imprécision dans la mesure de la longitude était source de retards, de maladies quand ce n'était pas de naufrages.

Parmi ces naufrages, l'un deux fut l'événement déclencheur d'une véritable « course à la longitude ».

Nous sommes en octobre 1707. Après avoir mené des combats victorieux à Gibraltar, l’amiral britannique Cloudesley Shovell met le cap sur l'Angleterre avec son escadre de cinq navires. Douze jours durant, il se fraye un chemin à travers un épais brouillard en direction de la Manche.

L’amiral et ses officiers pensent leur flotte en sécurité au large d'Ouessant. Mais ce sont en fait les îles Scilly qui se dressent devant eux dans la nuit du 22 octobre. Le navire amiral, l'Association, est le premier à percuter les rochers. Cette nuit-là, la Couronne britannique perd trois des cinq navires de guerre puisque l'EAgle et le Romney coulent aussi en heurtant les récifs. Les îles Scilly se transforment en tombeau pour 1 700 marins.

Quant à Cloudesley, il survécu au naufrage, se retrouva sur le sable... et fut tué par une femme qui passait par là. Tout simplement parce qu'elle voulait s'emparer (et s'empara) de l'émeraude qu'il portait au doigt.

Pressé (si on peut dire ! 7 ans après !) par une pétition signée des « Capitaines des vaisseaux de Sa Majesté, marchands de Londres et commandants des marchands » le Parlement publie, sous le règne de la reine Anne, le 8 juillet 1714 le Longitude Act ou Loi de longitude.

Le Longitude Act :

• Offrait trois prix :
  • 20 000 livres (5 millions de nos euros environ) pour une méthode de détermination de la longitude à 1/2 degré près de grand cercle) ce qui correspond à une variation maximum pour un chronomètre de trois secondes par 24 heures.
  • 15 000 livres pour une méthode précise aux 2/3 de degré près.
  • 10 000 livres pour une méthode précise au degré près.
• Désignait un juré (Conseil de longitude) chargé de l'attribution des prix. L'astronome royal y figurait comme membre d'office.
• Pouvait accorder des « avances ». Quand il fut dissous en 1828, il avait dépensé 100 000 livres.
• Vérifiait la mise à l'essai des « inventions » sur l'un des navires de Sa Majesté et "sur l'océan de la Grande-Bretagne vers n'importe quel port des Antilles que choisiraient les commissaires"

Cette offre n'était pas la première puisque, déjà en 1598, Philippe III d'Espagne en avait proposé une, en vain, au premier « découvreur de longitude ». Les Hollandais et Français firent aussi de même. Mais l'offre Anglaise était de loin la plus mirobolante.

Les solutions les plus farfelues avaient déjà été proposées avant le Longitude Act et ne manquèrent pas après.

Pour ne prendre qu'un exemple, la solution de la « poudre de sympathie » qui ne l'était d'ailleurs pas tellement. Cette poudre, découverte par un certain Kenelm Digby, domicilié dans le midi de la France, était censée guérir les blessures à distance. Il suffisait de l'appliquer sur un objet ayant été partie prenante à la blessure. Ce « traitement » était, parait-il particulièrement douloureux.

Trouver la longitude à l'aide de cette poudre était un jeu d'enfant. Blesser un chien. Lui prodiguer les premiers soins à une heure précise, midi par exemple. Embarquer le chien sur un navire et garder les pansements souillés à terre.

Vous avez compris le principe. Tous les jours, à midi, on met un peu de la fameuse poudre sur les pansements, le chien hurle du fait de ces soins « à distance » douloureux. On compare ce midi terrestre hurlant au midi sur le navire et il ne reste plus qu'à en déduire la longitude par calcul. Le risque, c'était que le chien guérisse vraiment en cours de navigation. Je plaisante, je plaisante.

Le « concours » est lancé et un certain John Harrison va entrer en scène.

On ne sait trop comment il a appris l'existence du prix offert mais tout le reste de sa vie va y être consacré.

L'histoire de sa vie, c'est un peu celle de la découverte de la mesure de la longitude. L'histoire de sa vie, c'est le roman d'une quête. Et je ne peux que vous conseiller la lecture du livre Longitude de Dava Sobel qui raconte justement la vie de Harrison comme un roman.

Évoquons-en quelques étapes ainsi que celles de la naissance de ces magnifiques chronomètres marins que sont H1, H2, H3 et H4.

Chronomètre marin contre méthode des distances lunaires, tout va opposer John Harrison (1693-1776) à gauche et Nevil Maskelyne (1732-1811) à droite dans la course à la longitude. Ces différences de vues vont vite tourner à une aversion partagée de l'un pour l'autre.

John Harrison et la course au prix

John Harrison est né le 24 mars 1693 dans le comté du Yorkshire.Son père lui apprend le métier de charpentier. Autodidacte, John plonge avec avidité dans une copie manuscrite d'une série de conférences données par le mathématicien Nicholas Saunderson.

À même pas 20 ans, en 1713, il construit sa première horloge en bois avec quelques éléments de cuivre et d'acier. Il tire le maximum des qualités des bois, roues en chêne, arbres et pignons en buis, coussinets en bois de gaïac. Ce sont les huiles du bois qui lubrifient les mouvements sans autre lubrification complémentaire.

Il invente un nouvel échappement, dit en sauterelle et un nouveau balancier, dit à gril, insensible à la température grâce à un judicieux mélange de métaux dont les dilatations se compensent.

Il construit aussi quelques horloges de parquet dont on voit un exemplaire à droite. Il y est aidé par son frère James qui, d'ailleurs, signe les horloges.

Il se marie en 1718 et son fils, né l'année suivante tombe malade et décède l'année suivante.

Il se remarie en 1726 et devient père de William, qui deviendra son bras droit, et d'Élisabeth.

Il conçoit un nouveau balancier en remplacement du gril qui ne résisterait pas aux conditions de navigation et, en 1730, persuadé qu'il a toutes les cartes techniques en main pour construire des horloges de marine, il se rend à Londres pour soumettre son projet au Conseil de la longitude.

Mais le Conseil, ne s'étant jamais réuni, n'avait pas de siège.

Il se rend donc chez un de ses membres, Edmund Halley (1656-1742), découvreur de la trajectoire de la comète qui porte son nom et alors astronome royal.

Halley est séduit par le projet d'Harrison mais il sait que le Conseil, qui regroupe des astronomes, des mathématiciens et des navigateurs, ne verra pas d'un bon œil une réponse mécanique au problème de la longitude.

Sagement, il l'adresse donc plutôt à l'horloger George Graham (1673 - 1751)

George Graham (à droite) reçoit Harrison à dix heures du matin et ne le laissera partir que tard dans la nuit après l'avoir invité à souper.

Après l'avoir aussi écouté, durant ces longues heures, expliquer son projet.

Harrison quittera l'Honnête George comme on l'appellera plus tard avec un protecteur et des capitaux offerts par Graham sans garantie ni intérêts.

Harrison passera les cinq années suivantes à construire H-1.

90 cm de hauteur, largeur et profondeur, 33 kilos, dents en bois, échappement silencieux à sauterelle, 4 quadrants (jours, heures, minutes, secondes), amas de tiges, ressorts, boules, molettes, telle est H-1 sans son boîtier en bois.

Et surtout, déjà, une précision prouvée dans un essai entre Londres et Lisbonne qui permet à Harrison, outre d'être malade comme un chien durant le voyage, de corriger de 140 km l'estime du capitaine. Pour la voir en photo, cliquez ici.

Au lieu de demander un essai Londres-Antilles comme le prévoit le Longitude Act, Harrison déclare que H-1 a quelques défauts et se contente de demander une avance pour concevoir une autre horloge. Il l'obtient, doit rajouter une clause à l'accord précisant qu'il devra « pour le bien public » remettre la future horloge et la précédente, et rentre chez lui pour se mettre à H-2

Harrison mettra quatre ans pour achever H-2.

Elle sera encore plus lourde que H-1.

Des essais la soumirent à des tortures diverses : changements de température, secousses pendant des heures. Bref, pire que les pires conditions qu'elle pourrait subir sur un navire. Des photos sont sur cette page.

La Royal Society conclut que "... le mouvement est suffisamment exact et régulier pour trouver la longitude d'un navire dans les termes les plus restreints tels qu'ils ont été proposés par le Parlement, et probablement mieux encore"

Elle ne connaîtra pourtant jamais la mer.

Parce qu'Harrison va refaire le coup des améliorations possibles comme il l'avait fait pour H-1.

Il veut construire H-3 et se contentera de demander, de temps à autre, des avances.

Harrison mettra onze ans pour achever H-3.

753 pièces, bande bi-métallique compensant les changements de température, nouveau système anti-friction, 7 kilos de moins que H-1, deux balanciers circulaires, réduite en dimensions, telle est H-3. Les photos sont à consulter en cliquant ici.

Elle ne connaîtra pas mieux la mer que H-2

Parce que Harrison a fait la connaissance de John Jefferys, horloger, qui lui fabrique une montre de gousset. Conçue d'après des indications d'Harrison en personne, elle est d'une fiabilité jamais connue à cette époque.

Harrison est persuadé que l'avenir est aux « petites machines » et se met à la conception de H-4.

Harrison achèvera en 1759 la construction de H-4.

13 centimètres de diamètre, trois aiguilles d'acier qui donnent l'heure exacte, diamants et rubis pour supprimer la friction, 30 heures entre deux remontages, telle est H-4. Une bête de concours. Consultez la page de musée royal de Greenwich pour voir de nombreuses photos.

Concours qu'elle gagnera... enfin presque.

Harrison a 66 ans losqu'il l'achève. Et il faudra qu'il attende sa 68 ème année pour que H-4 réponde aux conditions fixées par le Longitude Act à l'issue d'un voyage de Londres à la Jamaïque entre novembre 1761 et mars 1762. Et d'un nouvel essai vers la Barbade en 1764 qui fit ressortir 15 secondes de retard en 5 mois de voyage.

Harrison se trouvera pris dans une querelle qui l'opposera au Bureau des Longitudes pour obtenir la récompense promise par l'Act.

Querelle avec le Bureau des longitudes ? Lutte sans merci contre Nevil Maskelyne, devenu astronome royal, serait plus exact. Mais c'est une autre histoire.

Et comme cette page est consacrée aux instruments de mesure du temps, nous ne pouvons pas entrer dans les détails de la méthode des distances lunaires défendues mordicus, et c'est normal pour un astronome, par Maskelyne.

Dans son livre l'heure qu'il est, David S.Landes écrit :

Harrison finit par obtenir sa récompense, mais uniquement parce que le roi George III, lui-même horloger amateur (comme Louis XVI en France), intervint en sa faveur : « Par Dieu, Harrison, je vous ferais rendre justice ! ». C'est le Parlement qui lui vota la somme - ce qui n'empêcha tout de même pas le Bureau des Longitudes de le « flouer » des 1 250 livres qu'il lui avait versées pour H-2 et H-3 et qu'il décida de déduire de la somme qui lui était due. Voilà une fin aigre-douce à l'histoire d'une œuvre extraordinaire.

La fin de l'histoire ? Pas tout à fait.

Il faut rajouter que Harrison mourut en 1776.

Quant à ses chronomètres marins, ils sont toujours bien vivants au National Maritime Museum, Park Row, Greenwich, Londres. Seule H-4, qui nécessiterait un nettoyage tous les trois ans est arrêtée parce que cet entretien serait risqué.

En guise de conclusion

Il faut bien le dire, la méthode des distances lunaires donna aussi de bons résultats. Il fallait du temps et 4 personnes pour l'appliquer.

Comme les tables et un sextant ne coûtaient que 20 livres contre 100 pour K3 (une montre de « série » construite par Kendall), ces tables furent encore longtemps utilisées.

Harrison a-t-il inventé la longitude ? Certes pas. Il a tout simplement inventé des instruments de plus en plus précis permettant de mettre en œuvre les moyens de la calculer. Et, surtout, il a montré c'était techniquement possible.

Peu de ses innovations furent reprises par la suite, remplacées par des techniques moins chères, plus faciles à mettre en œuvre et plus efficaces.

Le GPS a maintenant remplacé les chronomètres marins. Ce n'est pas une raison pour oublier John Harrison qui a passé sa vie à montrer la voie...