- Accueil
- À ne pas manquer
- Calendriers Saga
- Études thématiques
- Les échelles de temps
Cette étude s'adresse à ceux qui tentent de construire des logiciels de conversion entre calendriers et à ceux qui veulent y voir plus clair dans les différentes abréviations et leur signification (UT, UTC, GMT, TE...). Comme cette page ne fait pas double emploi avec la page Astronomie, il est vivement conseillé de relire cette dernière avant de poursuivre la lecture de celle-ci. Les instruments de mesure du temps font l'objet d'une autre étude.
1) En quête d'une unité de temps - histoire de la seconde
Imaginons qu'on nous demande de définir la seconde. Comment allons-nous procéder ?
Tout naturellement, parmi les phénomènes astronomiques, nous allons en chercher un qui nous paraisse stable et dire que la seconde est la X ième partie de ce phénomène qui sera notre échelle de temps.
Bien entendu, la stabilité est une condition indispensable pour déterminer une bonne échelle de temps. Il ne serait pas très imaginable de définir une longueur d'élastique comme instrument de mesure du mètre.
A) Première étape de notre quête
La première idée qui vient à l'esprit est de prendre la longueur du jour comme échelle de temps. Il suffit donc de définir le jour comme étant la durée qui sépare deux passages consécutifs du Soleil à son point culminant, c'est-à-dire au «méridien» d'un lieu. Cette mesure étant une mesure instantanée à un jour précis, nous venons de définir le jour solaire vrai. Pour tout dire, c'est l'heure des cadrans solaires.
Malheureusement, nous n'allons pas pouvoir tenir compte de ce jour solaire vrai parce sa durée varie au cours de l'année. Par exemple, à Paris, la durée entre deux passages au méridien sera de 23 h 59 min 47 s entre le 21 mars et le 22 mars. En revanche, elle passera à 24 h 00 min 00 s entre le 1 janvier et le 2 janvier.
Cette différence est la conséquence de deux phénomènes :
- L'orbite de la Terre est elliptique et soumise aux lois de Képler (cf. page Astronomie)
- La projection géométrique sur l'équateur céleste se déplace plus rapidement aux solstices qu'aux équinoxes.
Nous ne pouvons donc pas utiliser le jour solaire vrai pour définir notre seconde. Essayons autre chose.
Nous allons imaginer un «Soleil fictif» qui, au lieu de parcourir l'écliptique, va parcourir l'équateur dans un mouvement constant et circulaire. Nous avons défini ainsi un temps solaire moyen et le jour solaire moyen sera défini comme précédemment.
Si on compare les tableaux de levers et de couchers du soleil de plusieurs calendriers des Postes établis sur le principe du jour solaire moyen, on constatera l'équivalence des chiffres jour à jour. Nous tenons donc notre échelle de temps fiable qui a pour nom Temps universel dont l'abréviation est T.U. (ou U.T. en anglais). Universel signifie que le temps est donné par la rotation de la Terre. L'heure donnée dans l'échelle U.T. est tout simplement celle de nos montres.
Première définition de la seconde
Nous avons bien travaillé puisqu'une première définition de la seconde correspondait bien à la X ème partie du jour solaire moyen :
La seconde est la 1/86 400 ème partie du jour solaire moyen
L'échelle de temps correspondante était définie comme suit : Le Temps Universel UT est le temps solaire moyen pour le méridien origine augmenté de 12 heures. Nous reviendrons plus loin sur la notion de méridien origine.
Quelques remarques avant de passer à la suite de notre histoire de la seconde :
Première remarque
Reprenons un instant notre calendrier des Postes et notons les heures de lever et de coucher du Soleil à une date quelconque : pour le premier janvier 2002 par exemple, nous aurons 07 46 et 16 02. Faisons la demi somme de ces deux heures et nous obtiendrons l'heure de passage au méridien de notre Soleil fictif : 11 h 54 min 30 s d'où un écart de 5 min 30 s par rapport au temps solaire moyen. Le Soleil ne passe donc pas au méridien à 12 h T.U. mais soit en avant, soit après.
Si on reporte tous ces écarts journaliers sur un graphe, on obtient une courbe qui porte le nom d'équation du temps.
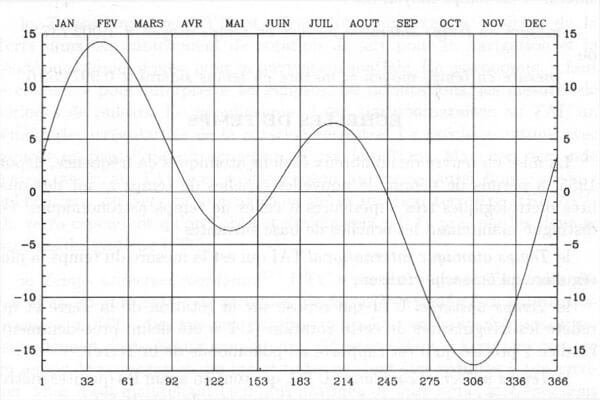
Cette courbe s'annule quatre fois dans l'année (16 avril, 14 juin, 1 septembre, 25 décembre). Si nous refaisons notre demi-somme lever/coucher pour ces dates d'après notre calendrier des postes, nous constatons bien que le passage du soleil au méridien passe bien... 9 minutes avant 12 h T.U !! Pourquoi ces 9 minutes ? Tout simplement parce que le calendrier des Postes donne l'heure au passage du méridien de Paris et non pas au «méridien origine» (Greenwich) dont il est question dans la définition donnée plus haut. C'est une vieille histoire que nous évoquerons plus loin dans cette page.
À l'aide de cette courbe, on peut passer du Temps moyen au Temps vrai et inversement :
Temps moyen = Temps vrai + Équation du temps
La courbe de l'équation du temps est souvent représentée sous une autre forme (analemme) sur ou à proximité des cadrans solaires pour permettre de procéder à la correction temps moyen/temps vrai

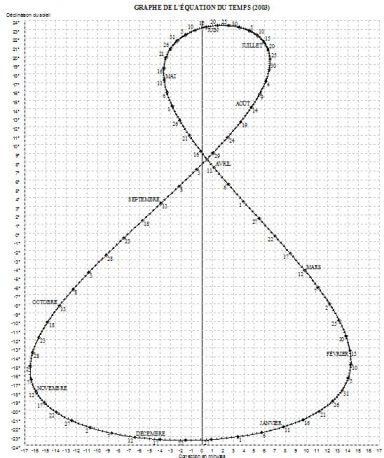
L'équation du temps telle qu'elle se présente sous forme d'analemme.
Seconde remarque
Dès 1955, plusieurs variantes de U.T. ont été déclinées :
- TU0 (ou UT0) est le temps universel brut de tous correctifs. Précision de l'ordre de 0,1 seconde
- TU1 (ou UT1) tient compte du mouvement des pôles (position de l'axe de rotation instantané de la Terre). C'est l'ancien UT. Précision de l'ordre de 1 ms (0,001 seconde)
- TU2 (ou UT2) tient compte des variations annuelles de la rotation de la Terre dues aux grands événements climatiques.
- TU3 (ou UT3) tient compte des effets lunaires (attraction, marées...)
Notons au passage que, pour nous qui traitons des calendriers et pour beaucoup d'autres, il n'y a pas de quoi se prendre la tête entre ces différents TUx puisque l'écart entre eux est minime (moins de 30 millisecondes entre TU1 et TU0 ; moins de 60 millisecondes entre TU2 et TU1 ; moins de 4 millisecondes entre TU3 et TU2).
Nous parlerons plus loin de UTC qui a vu le jour plus tard.
Troisième remarque : mais, allez-vous me dire, pourquoi ne parle-t-on pas de GMT ? Eh bien, parlons-en !!
GMT est une abréviation pour Greenwich Mean Time (Temps moyen de Greenwich) qui est le Temps moyen au méridien zéro qui est le méridien de Greenwich. Nous reviendrons dans la deuxième partie sur ce choix du méridien zéro.
Cette unité de temps n'a plus de raison d'être depuis 1925, année où elle a été remplacée par U.T et, pour être plus précis, par UT1. Mais il semble qu'elle ait la peau dure dans certains milieux professionnels. Ceci étant dit, nous n'avons pas trop de leçons à donner quand on voit que le calendrier des Postes donne toujours les levers et couchers du soleil relevées au méridien de... Paris qui n'est pas le méridien zéro reconnu dans le monde entier.

Le site de Greenwich fut connu sous le nom de Old Greenwich Observatory et ses bâtiments furent intégrés au National Maritime Museum.
En fin de compte, l'observatoire de Greenwich ne porta son nom qu'en quittant Greenwich.
Si on parcourt les groupes de discussion sur le web, on constate qu'il naît des échanges sans fin sur l'heure GMT. Certains avancent avec certitude que UT = GMT. D'autres, non moins certains d'eux-mêmes, certifient que UT = GMT + 12 h.
Qui a raison dans cette histoire ? La réponse est simple : TU1 = GMT + 12 h. Lorsque le Soleil moyen passe au dessus du méridien de Greenwich, il est 00 h 00 GMT et, suivant la définition de UT, il est 00 h 00 + 12 h 00 = 12 h 00.
La polémique vient du fait que certains corps de métier (astronomes, navigateurs...) avaient jugé bon de convenir, pour ne pas changer de journée en plein milieu de leur travail nocturne, qu'à «midi» GMT, il serait 00 h 00. Mais c'était détourner la définition de GMT. C'est une fausse polémique puisque GMT n'existe plus.
B) Seconde étape de notre quête
Lorsqu'on compare le Temps solaire moyen d'une année à la suivante, nous n'avons aucune raison de ne pas être fiers de notre découverte de l'échelle de temps UT basée sur la rotation de la Terre.
Malheureusement, il nous va falloir déchanter et nous remettre à la recherche d'une nouvelle échelle : la Terre ralentit dans sa rotation au fil des siècles. Tous les astronomes l'ont constaté un jour où l'autre et Halley (1656-1742) qui a découvert la comète portant son nom s'en doutait déjà quand il constata que ses observations ne correspondaient pas à ses calculs.
Essayons de comprendre ce phénomène de ralentissement dont la principale coupable est la Lune :
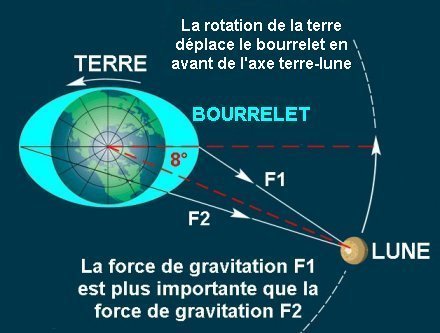
L'effet de marée dû à l'attraction lunaire déforme la terre en une ellipse. Il s'agit aussi bien des marées que nous connaissons mais aussi d'une «marée terrestre» qui déforme la Terre de quelques centimètres. Le grand axe de cette ellipse devrait passer par le centre de la Lune. Mais ce serait ne pas tenir compte de la rotation de la terre sur elle-même que de penser ainsi. Et comme la Terre tourne sur elle-même plus vite que la Lune autour d'elle, les bourrelets formés par les marées ne pointent pas sur la Lune mais sont «en avance» sur elle. L'angle formé est d'environ 8 degrés.
Ces deux bourrelets exercent deux forces d'inégale intensité sur la Lune (voir image ci-dessous). La résultante de ces deux forces a un double effet :
- La rotation de la Terre est ralentie. Le jour s'allonge d'environ 1,8 millisecondes par siècle.
- À l'inverse la Lune est accélérée. Et, dans l'espace, qui dit accélération dit changement d'orbite : la Lune s'éloigne de la Terre. Cet éloignement mesuré est de deux à trois centimètres par an.
Ces phénomènes vont-ils durer indéfiniment ? Non, ils vont se stabiliser dès que la rotation de la Terre et de la Lune seront synchrones. À ce moment là, dans quelques milliards d'années, la Lune et la Terre ne se présenteront l'une l'autre que la même face et la longueur du jour terrestre sera égale à la longueur du mois lunaire. Ce serait de l'ordre de 50 jours actuels. Notons au passage que la Lune a déjà terminé son phénomène de synchronisation puisque la durée de sa rotation est égale à sa durée de révolution.
Notons également que si la journée sur Terre s'allonge, elle a aussi été beaucoup plus courte. Les dinosaures, par exemple, connaissaient une journée de 20 heures.
Le plus étonnant est qu'il existe des témoins de ces phénomènes : les Nautiles.
Le Nautile est un mollusque possédant une coquille cloisonnée enroulée en spirale. Les compartiments sont reliés entre eux par un minuscule tube et, chaque nuit, le nautile injecte une quantité d'azote dans ces compartiments ce qui a pour effet de le faire remonter des 400 mètres de profondeur où il vit jusqu'à la surface.

A chacune de ces remontées, le Nautile sécrète une strie de carbonate de calcium composant la coquille. Ces stries restent visibles. Au bout de 29 ou 30 jours une nouvelle cloison est constituée.
Deux chercheurs, G. Kahn, de Princeton University, et S. Pompea, de Colorado States University, en ont conclu que le Nautile obturerait donc une nouvelle chambre chaque mois lunaire, tout comme nos arbres forment un nouveau cerne chaque année (publication dans Nature vol 275, pages 606–611, 1978).
En remontant le temps et en examinant des fossiles de spécimens différents mais présentant les mêmes caractéristiques de vie, Kahn et Pompea ont alors étudié des Nautiles fossiles de près de 420 millions d'année constatèrent que le nombre de stries par compartiment était d'autant plus faible que les spécimens étaient anciens : 25 stries pour des spécimens vieux de 30 millions d'années, 17 pour des spécimens de 150 millions d'années et 9 pour 420 millions d'années.
On peut en conclure qu'il y a 420 millions d'années la Lune tournait vraisemblablement autour de la Terre en 9 jours. Selon la 3ème Loi de Képler la distance Terre-Lune était alors seulement de 150.000 kilomètres.
Après avoir plongé au fond des océans à la recherche de preuves, nous sommes maintenant convaincus que notre échelle de temps initiale (TU) n'est pas fiable. Il nous faut en trouver une autre.
Puisque nous avons échoué avec la journée, pourquoi ne pas essayer un phénomène astronomique bien connu : l'année.
C'est en 1960 que la onzième conférence générale des poids et mesures décide de définir une nouvelle échelle de temps basée sur la longueur de l'année : Le temps des Éphémérides.
Accrochons nous et admirons la simplicité de la définition de cette échelle de temps :
Le Temps des Éphémérides TE est obtenu comme solution de l'équation qui donne la longitude moyenne géométrique du Soleil :
L = 279°41'48,04" + 129.602.768,13« T + 1,089» T2
où T est compté en siècles juliens de 36525 jours des éphémérides. L'origine de T est datée le 0 janvier 1900 à 12h TE, à l'instant où la longitude moyenne du Soleil a pris la valeur 279°41'48,04".
Et on en arrive à la deuxième définition de la seconde :
La seconde est la fraction 1/31.556.925,9747 de l'année tropique pour 1900 janvier 0 à 12 heures de temps des éphémérides.
- Première remarque : Elle est toute personnelle, je n'y ai rien compris.
- Deuxième remarque : Son utilisation s'est limitée aux seuls moyens astronomiques.
- Troisième remarque : Cette définition de la seconde n'a duré que jusqu'en 1967.
- Quatrième remarque : Compte tenu des deux remarques qui précèdent, on ne va pas se prendre la tête et on passe à la suite.
C) Troisième et dernière étape de notre quête
Ce n'est pas dans la rotation de la Terre ni dans sa révolution autour du Soleil que nous allons trouver la réponse à la question qui nous a été posée : définir le seconde. C'est dans l'infiniment petit : l'atome.
Suite à des travaux réalisés en 1955 par deux physiciens L.Essen et J.Parry du National Physical Laboratory de Londres, on en arrive en 1967 (lors de la treizième conférence nationale des poids et mesures) à une troisième définition de la seconde :
La seconde est la durée de 9.192.631.770 périodes de la radiation correspondant à la transition entre les deux niveaux hyperfins de l'état fondamental de l'atome de Césium 133.
et à une nouvelle échelle de temps : le Temps Atomique International (T.A.I).
Passons sur les détails techniques qui ne nous concernent pas beaucoup puisque ce TAI est utilisé pour des travaux scientifiques plutôt que dans la vie courante et est sans utilité dans la conception des calendriers. Sachons simplement qu'il est fourni par 200 horloges réparties dans 30 pays et comparées entre elles régulièrement grâce à l'utilisation «à l'envers» du Global Positioning System (GPS). Admirons aussi la précision de ce temps qui est estimée à 1 seconde pour 1 500 000 ans.
Et nous en arrivons à l'essentiel. Même si UT1 présente des irrégularités, c'est quand même bien la rotation de la Terre qui rythme nos jours et nos nuits. Il serait dommage, sous prétexte d'avoir une seconde stable, de voir le Soleil au zénith... à 15 h 00 par exemple !
Plusieurs choses ont donc été faites lors de l'adoption du TAI :
- On a décidé d'instaurer, le 1 janvier 1972, un temps universel standard qui serait la base de l'heure légale dans le monde. C'est l'universal time coordinated (temps universel coordonné) U.T.C. Depuis 1978, c'est le temps légal en France.
- Son origine a été définie de telle sorte que UT1 - TAI soit égal à zéro le premier janvier 1958.
Il ne faut voir dans U.T.C qu'une variante de UT1 à laquelle elle est intimement liée. C'est un compromis entre TAI et UT1 puisque, même si son unité de temps est la seconde TAI, elle ne peut s'éloigner de UT1 de plus ou moins de 0,9 seconde.
Comment maintenir cet écart maximum ? Le Service International de la Rotation de la Terre (International Earth Rotation Service,IERS et anciennement Bureau International de l'Heure) à Paris surveille cet écart et intercale ou retranche une seconde à l'UTC. Cette correction se fait soit le 30 juin, soit le 31 décembre à minuit. La minute compte donc 61 secondes et nos montres...avancent d'une seconde. Il ne nous reste plus qu'à les remettre à l'heure.
Le 1 janvier 1972, la différence TAI-UTC était de 10 secondes. Depuis, 23 secondes ont été rajoutées et la différence TAI-UTC est actuellement de 33 secondes et passera à 34 secondes en 2009.
Les sauts de secondes sont annoncés dans le Bulletin C. Voici celui 2008 :
INTERNATIONAL EARTH ROTATION AND REFERENCE SYSTEMS SERVICE (IERS)
SERVICE INTERNATIONAL DE LA ROTATION TERRESTRE ET DES SYSTEMES DE REFERENCE
SERVICE DE LA ROTATION TERRESTRE
OBSERVATOIRE DE PARIS
61, Av. de l'Observatoire 75014 PARIS (France)
Tel. : 33 (0) 1 40 51 22 26
FAX : 33 (0) 1 40 51 22 91
e-mail : services.iers@obspm.fr
http://hpiers.obspm.fr/eop-pcParis, 4 July 2008
Bulletin C 36
To authorities responsible
for the measurement and
distribution of timeUTC TIME STEP
on the 1st of January 2009A positive leap second will be introduced at the end of December 2008.
The sequence of dates of the UTC second markers will be:2008 December 31, 23h 59m 59s
2008 December 31, 23h 59m 60s
2009 January 1, 0h 0m 0sThe difference between UTC and the International Atomic Time TAI is:
from 2006 January 1, 0h UTC, to 2009 January 1 0h UTC : UTC-TAI = - 33s
from 2009 January 1, 0h UTC, until further notice : UTC-TAI = - 34sLeap seconds can be introduced in UTC at the end of the months of December
or June, depending on the evolution of UT1-TAI. Bulletin C is mailed every
six months, either to announce a time step in UTC or to confirm that there
will be no time step at the next possible date.Daniel GAMBIS
Head
Earth Orientation Center of IERS
Observatoire de Paris, France
Depuis 1972, une seconde a été rajoutée à chacune des années suivantes : 1972, 1973, 1974, 1975, 1976, 1977, 1978, 1979, 1980, 1981, 1982, 1984, 1987, 1989, 1990, 1991, 1992, 1993, 1995, 1996, 1998, 2005, 2008.
Notons au passage qu'auncune seconde n'a été rajoutée en 2009, juin 2010 et qu'aucune ne le sera en décembre 2010.
2) Histoire et fonctionnement des fuseaux horaires
Une notion beaucoup utilisée dans les calendriers (pour les conversions) est celle d'heure légale (ou heure locale) qui nous vient de la création des fuseaux horaires.
En 1875, lors d'un Congrès international à Paris, il est convenu de choisir un méridien unique a partir duquel on compterait les longitudes. Le méridien de Greenwich est choisi à la Conférence de Rome en 1883.
En 1884, la conférence internationale du méridien à Washington créé les fuseaux horaires : 24 bandes verticales de 15° de longitude de largeur. Certains pays, dont le France s'opposent à l'adoption du zéro de Greenwich.

C'est en 1878 que l'ingénieur écossais Sir Sanford Fleming (1827-1915), ingénieur-chef des chemins de fer canadiens proposa le système de fuseaux horaires que nous utilisons aujourd'hui.
Jusqu'en 1891, l'heure est variable en France puisque les horloges marquent le temps solaire moyen de la préfecture. Mais le développement des moyens de communication (train notamment) rend urgente l'utilisation d'une heure unique sur le territoire.
Cette heure unique est fixée par une loi du 14 mars 1891 : L'heure légale en France et en Algérie est le temps moyen de Paris.
Une parenthèse pour vous citer le texte qu'on peut lire dans une revue des sciences de l'époque, l'hebdomadaire La Nature : "...Pour la facilité du service et pour éviter les contestations d'heure avec les voyageurs, la plupart des compagnies vont mettre leurs appareils chronométriques sur lesquels elles règlent leur service, en retard de trois à cinq minutes sur l'heure du méridien de Paris ; de telle sorte que dans une gare, tous les cadrans placés à l'extérieur de la gare ou des guichets sont à l'heure de Paris, et les cadrans placés à l'intérieur de la gare sur les voies, sont en retard de cinq minutes ; tel est le cas pour les chemins de fer de Paris-Lyon-Méditerranée, de l'Ouest, de l'Etat, du Midi. Pour les chemins de fer du Nord et de l'Est, le retard n'est que de trois minutes..."
Par loi du 9 mars 1911, la France entre presque «dans le rang» et l'heure légale y devient l'heure du temps moyen de Paris retardée de 9 minutes 21 secondes (longitude de Paris). Cette définition voulait signifier en fait que l'heure en France était le temps universel.
La loi de 1911 a été remplacée par le décret du 9 août 1978 qui stipule que "le temps légal est obtenu en ajoutant ou en retranchant un nombre entier d'heures au temps universel coordonné".
Fonctionnement
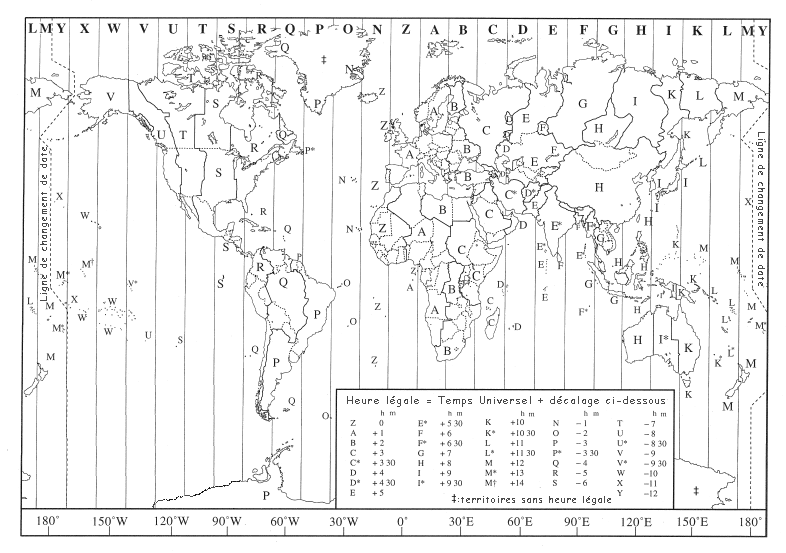
Regardons une carte sur laquelle figurent les fuseaux horaires :
Nous voyons d'abord les 24 «bandes» qui symbolisent les fuseaux horaires. En haut de chaque bande figure une lettre qui le caractérise. La bande Z correspond à celle qui contient le méridien de Greenwich qui, nous l'avons vu, correspond au méridien zéro. Si on poursuit ce méridien à son antipode (longitude 180°), on se trouve sur la ligne du changement de date. Quand on y regarde de plus près, on comprend mieux pourquoi le méridien de Greenwich a été choisi comme méridien zéro. Si on avait choisi, par exemple, le méridien de Paris, une partie de la Nouvelle Zélande vivrait sous deux jours différents. Quoique...
Il y a une heure de décalage entre un fuseau horaire et un autre. Lorsqu'on se déplace vers l'Est à partir du méridien zéro (Greenwich), il faut ajouter une heure à chaque changement de fuseau pour obtenir l'heure locale. À contrario, lorsqu'on se déplace vers l'ouest à partir du méridien zéro, il faut enlever une heure. Quand on arrive au méridien antipode du méridien zéro, on garde la même heure mais on change de jour dans un sens ou dans l'autre suivant d'où on vient.
Pour résumer, l'heure locale est la même dans un fuseau horaire donné, mais l'heure dans chaque fuseau est une heure plus tôt que dans le fuseau voisin à l'Est. Sans oublier la particularité de la ligne de date internationale. C'est grâce à elle que Phileas Fogg a gagné un jour dans son Tour du monde en quatre-vingts jours.
Voilà pour la théorie. Parce que, dans la pratique (pour voir une carte grand format cliquez ici) :
- Certains territoires comme le Groenland ou l'Antarctique n'ont pas d'heure légale propre: le Temps Universel Compensé y est donc utilisé.
- Les bords des fuseaux ne sont pas linéaires : certains pays, en effet, se refusent à être à cheval sur deux fuseaux. Les lignes des fuseaux suivent donc souvent les frontières. Quelquefois même, les fuseaux sont redessinés à l'intérieur d'un pays (Canada par exemple). Même la ligne de partage des dates n'échappe pas à quelques modifications.
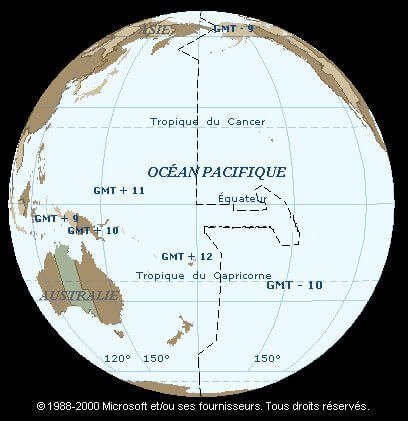
La ligne de séparation des dates n'est pas linéaire. Notons au passage que certains n'hésitent pas à parler encore GMT.
- À contrario, certains pays qui devraient comporter plusieurs heures légales puisqu'englobant plusieurs fuseaux horaires ont décidé de n'utiliser qu'une heure légale pour tout le pays. C'est le cas de la Chine qui observe l'heure légale de Pékin, la capitale.
- D'autres pays, eux, utilisent leur propre heure locale (Afghanistan = +3.5 ; Inde = +5.30 ; Népal = +5.45...). la France n'est pas en reste puisque, bien que située intégralement dans le fuseau zéro, elle accuse +1.00. Décidément, nous avons du mal à nous faire à Greenwich !!
- A tout cela, il nous faut rajouter un peu partout le système des heures d'été/d'hiver (D.S.T Daylight Saving Time). En ce qui concerne la France, voici l'Arrêté du 3 avril 2001 relatif à l'heure légale française signé par Laurent Fabius :
Le ministre de l'économie, des finances et de l'industrie, le ministre de l'équipement, des transports et du logement et le secrétaire d'Etat à l'industrie,
Vu la directive 2000/84/CE du Parlement européen et du Conseil du 19 janvier 2001 concernant les dispositions relatives à l'heure d'été ;
Vu le décret no 78-855 du 9 août 1978 relatif à l'heure légale française ;
Vu le décret no 79-896 du 17 octobre 1979 fixant l'heure légale française,
Arrêtent :Art. 1er. - Dans les départements métropolitains de la République française, à compter de l'année 2002 et pour les années suivantes, la période de l'heure d'été commence le dernier dimanche du mois de mars à 2 heures du matin. À cet instant, il est ajouté une heure à l'heure légale.
Art. 2. - Dans les départements métropolitains de la République française, à compter de l'année 2002 et pour les années suivantes, la période de l'heure d'été se termine le dernier dimanche du mois d'octobre à 3 heures du matin. À cet instant, il est retranché une heure à l'heure légale.
Art. 3. - Le présent arrêté sera publié au Journal officiel de la République française.
Un petit tableau non exhaustif des heures légales dans différents pays (sans tenir compte des heures d'été/d'hiver). Note : ce tableau n'est plus à jour, les pays changent parfois de fuseau horaire.
| A | G | O | |||
| Afghanistan | + 4.5 H | Gabon | + 1.0 H | Oman | + 4.0 H |
| Afrique du Sud | + 2.0 H | Gambie | + 0.0 H | P | |
| Albanie | + 1.0 H | Géorgie | + 4.0 H | Pakistan | + 5.0 H |
| Algérie | + 1.0 H | Ghana | + 0.0 H | Panama | - 5.0 H |
| Allemagne | + 1.0 H | Grèce | + 2.0 H | Papouasie - Nouvelle Guinée | + 10.0 H |
| Andorre | + 1.0 H | Grenade | - 4.0 H | Paraguay | - 4.0 H |
| Angola | + 1.0 H | Guatemala | - 6.0 H | Pays-Bas | + 1.0 H |
| Antigua-et-Barbuda | - 4.0 H | Guinée | + 0.0 H | Pérou | - 5.0 H |
| Arabie saoudite | + 3.0 H | Guinée équatoriale | + 0.0 H | Philippines | + 8.0 H |
| Argentine | - 2.0 H | Guinée-Bissao | + 0.0 H | Pologne | + 1.0 H |
| Arménie | + 4.0 H | Guyana | - 3.0 H | Portugal | + 1.0 H |
| Australie | + 10.0 H | H | Q | ||
| Autriche | + 1.0 H | Haïti | - 5.0 H | Qatar | + 3.0 H |
| Azerbaïdjan | + 3.0 H | Honduras | - 6.0 H | R | |
| B | Hongrie | + 1.0 H | République Centrafricaine | + 0.0 H | |
| Bahamas | - 5.0 H | I | République Dominicaine | - 4.0 H | |
| Bahreïn | + 3.0 H | Inde | + 5.5 H | République Tchèque | + 2.0 H |
| Bangladesh | + 6.0 H | Indonésie | + 8.0 H | Réunion | + 4.0 H |
| Belgique | + 1.0 H | Iran | + 3.5 H | Roumanie | + 2.0 H |
| Belize | - 6.0 H | Iraq | + 3.0 H | Royaume-Uni | + 0.0 H |
| Bénin | + 1.0 H | Irlande | + 0.0 H | Russie Centre | + 4.0 H |
| Bhoutan | + 6.0 H | Islande | + 0.0 H | Russie Est | + 11.0 H |
| Birmanie | + 6.5 H | Israël | + 2.0 H | Russie West | + 2.0 H |
| Bolivie | - 4.0 H | Italie | + 1.0 H | Rwanda | + 2.0 H |
| Bosnie-Herzégovine | + 1.0 H | J | S | ||
| Botswana | + 2.0 H | Jamaïque | - 5.0 H | Saint-Christophe-et-Niévès | - 4.0 H |
| Brésil | - 4.0 H | Japon | + 9.0 H | Sainte-Lucie | - 4.0 H |
| Brunei | + 8.0 H | Jordanie | + 2.0 H | Saint-Marin | - 4.0 H |
| Bulgarie | + 2.0 H | K | Saint-Vincent-et-les Grenadines | - 4.0 H | |
| Burkina | + 0.0 H | Kazakhstan | + 6.0 H | Salomon | + 11.0 H |
| Burundi | + 2.0 H | Kenya | + 3.0 H | Samoa occidentales | - 11.0 H |
| C | Kiribati | + 12.0 H | Sao Tomé-et-Principe | + 0.0 H | |
| Cambodge | + 7.0 H | Koweït | + 3.0 H | Sénégal | + 0.0 H |
| Cameroun | + 1.0 H | L | Seychelles | + 4.0 H | |
| Canada Centre | - 6.0 H | Laos | + 7.0 H | Sierra Leone | + 0.0 H |
| Canada Est | - 5.0 H | Lesotho | + 2.0 H | Singapour | + 8.0 H |
| Canada Montagnes | - 7.0 H | Lettonie | + 2.0 H | Slovaquie | + 1.0 H |
| Canada Pacific | - 8.0 H | Liban | + 2.0 H | Slovénie | + 1.0 H |
| Cap-Vert | - 1.0 H | Liberia | + 0.0 H | Somalie | + 3.0 H |
| Chili | - 4.0 H | Libye | + 2.0 H | Soudan | + 2.0 H |
| Chine | + 8.0 H | Liechtenstein | + 1.0 H | Sri Lanka | + 5.5 H |
| Chypre | + 2.0 H | Lituanie | + 2.0 H | Suède | + 1.0 H |
| Colombie | - 5.0 H | Luxembourg | + 1.0 H | Suisse | + 1.0 H |
| Congo | + 1.0 H | M | Suriname | - 3.0 H | |
| Cook | - 10.0 H | Macédoine | + 1.0 H | Swaziland | + 2.0 H |
| Corée du Nord | + 9.0 H | Madagascar | + 3.0 H | Syrie | + 2.0 H |
| Corée du Sud | + 9.0 H | Malaisie | + 8.0 H | T | |
| Costa Rica | - 6.0 H | Malawi | + 2.0 H | Tadjikistan | + 6.0 H |
| Côte d'Ivoire | + 1.0 H | Maldives | + 5.0 H | Taiwan | + 8.0 H |
| Croatie | + 1.0 H | Mali | + 0.0 H | Tanzanie | + 3.0 H |
| Cuba | - 5.0 H | Malte | + 1.0 H | Tchad | + 1.0 H |
| D | Maroc | + 0.0 H | Thaïlande | + 7.0 H | |
| Danemark | + 1.0 H | Marshall | + 12.0 H | Togo | + 0.0 H |
| Djibouti | + 3.0 H | Maurice | + 4.0 H | Tonga | + 13.0 H |
| Dominique | - 4.0 H | Mauritanie | + 0.0 H | Trinité-et-Tobago | - 4.0 H |
| E | Mexique Centre | - 6.0 H | Tunisie | + 1.0 H | |
| Égypte | + 2.0 H | Mexique Est | - 5.0 H | Turkménistan | + 5.0 H |
| Émirats arabes unis | + 4.0 H | Mexique West | - 7.0 H | Turquie | + 2.0 H |
| Équateur | + 1.0 H | Moldavie | + 2.0 H | Tuvalu | + 12.0 H |
| Érythrée | + 3.0 H | Monaco | + 1.0 H | U | |
| Espagne | + 1.0 H | Mongolie | + 8.0 H | Uganda | + 3.0 H |
| Estonie | + 2.0 H | Mozambique | + 2.0 H | Ukraine | + 2.0 H |
| États-Unis CT | - 7.0 H | N | Uruguay | - 3.0 H | |
| États-Unis EST | - 6.0 H | Namibie | + 1.0 H | V | |
| États-Unis MT | - 8.0 H | Nauru | + 12.0 H | Vanuatu | + 11.0 H |
| États-Unis PCT | - 9.0 H | Népal | + 5.75 H | Vatican | + 1.0 H |
| Éthiopie | + 3.0 H | Nicaragua | - 6.0 H | Venezuela | - 4.0 H |
| F | Niger | + 1.0 H | Viêt Nam | + 7.0 H | |
| Fidji | + 12.0 H | Nigeria | + 1.0 H | W | |
| Finlande | + 2.0 H | Norvège | + 1.0 H | Wallis And Futuna Islands | + 12.0 H |
| France | + 1.0 H | Nouvelle-Zélande | + 12.0 H | Y | |
| Rappel : ce tableau ne tient pas compte des heures d'été et d'hiver | Yémen | + 3.0 H | |||
| Yougoslavie | + 1.0 H | ||||
| Z | |||||
| Zambie | + 2.0 H | ||||
| Zimbabwe | + 2.0 H | ||||
Et, pour terminer, un gadget : la liste des mots qui correspondent aux lettres des fuseaux horaires :
| Lettre | Mot | Heure locale |
|---|---|---|
| Y | Yankee | UTC - 12 |
| X | X-Ray | UTC - 11 |
| W | Wisky | UTC - 10 |
| V | Victor | UTC - 9 |
| U | Uniform | UTC - 8 |
| T | Tango | UTC - 7 |
| S | Sierra | UTC - 6 |
| R | Roméo | UTC - 5 |
| Q | Quebec | UTC - 4 |
| P | Papa | UTC - 3 |
| O | Oscar | UTC - 2 |
| N | November | UTC - 1 |
| Z | Zoulou | UTC |
| A | Alpha | UTC + 1 |
| B | Bravo | UTC + 2 |
| C | Charlie | UTC + 3 |
| D | Delta | UTC + 4 |
| E | Echo | UTC + 5 |
| F | Fox-trot | UTC + 6 |
| G | Golf | UTC + 7 |
| H | Hotel | UTC + 8 |
| I | India | UTC + 9 |
| K | Kilo | UTC + 10 |
| L | Lima | UTC + 11 |
| M | Mike | UTC + 12 |