- Accueil
- À ne pas manquer
- Calendriers Saga
- Les calendriers
- Le calendrier grec Attique
Un peu d'histoire
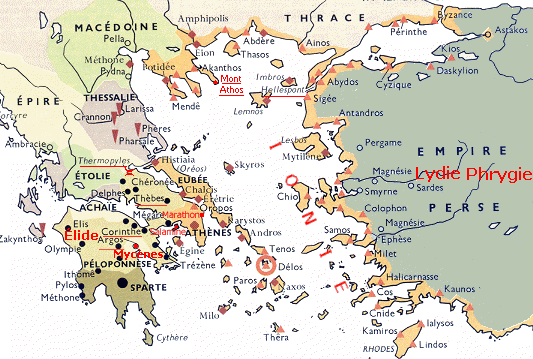
Afin de repérer les différents événements relatifs au calendrier en Grèce, nous allons voir rapidement les grandes périodes de l'antiquité en Grèce puis une chronologie un peu plus détaillée jusqu'à la mort d'Alexandre le Grand. Les événements concernant directement le calendrier seront notés en rouge.
Les grandes périodes de la Grèce antique
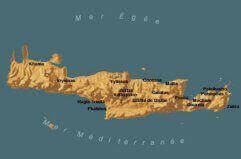
| Période néolithique | ~6500 à ~3200 | Cliquer sur les vignettes pour voir les cartes à une plus grande échelle | |
| Période du bronze Cette période est divisée en 3 parties : - Bronze ancien : 3200-1950 - Bronze moyen : 1950-1550 - Bronze moderne : 1550-1100 qui correspondent approximativement aux trois civilisations |
Civilisation cycladique | ~3200 à ~1950 | |
| Civilisation minoenne (Crète) |
~1400 à ~1200 | ||
| Civilisation mycénienne ou helladique | ~1400 à ~1200 | ||
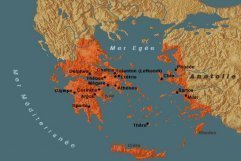
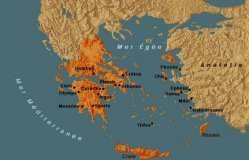
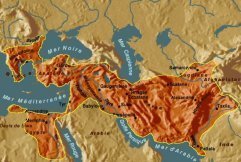
| Âges obscurs | Époque proto-géométrique | fin XIe siècle à IXe siècle | Cliquer sur les vignettes pour voir les cartes à une plus grande échelle |
| Époque géométrique | IXe et VIII siècles | ||
| Période orientaliste | ~720 à ~620 | ||
| Période archaïque | ~620 à ~490 | ||
| Période préclassique | ~490 à ~460 | ||
| Période classique | ~480 à ~323 | ||
| Période hellénistique | ~323 à ~31 |
Chronologie un peu plus détaillée
Les événements liés directement au calendrier sont en gras. Bien entendu, toutes les dates sont avant J.-C.
| Années (av. J.-C.) | Description |
|---|---|
| 6218 +/-150 | Site néolithique à Nicomèdes en Macédoine |
| 5520 +/-70 | Site à Drakhmani en Grèce centrale |
| 4480 | site néolithique près de Sesklo dans le sud de la Thessalie |
| 3000 à 1400 | Crète minoenne |
| 2500 à 1100 | Civilisation helladique dans le Péloponnèse |
| 2000 à 1600 | Les Ioniens occupent l’Attique et les Cyclades Les Éoliens s’établissent en Thessalie Les Achéens s’installent dans le Péloponnèse |
| 1480 à 1450 | Différence de culture entre Cnossos et le reste de la Crète |
| 1480 à 1450 | Occupation de Cnossos par les Mycéniens |
| 1400 | Destruction de Cnossos |
| 1260 | Destruction de Troie |
| 1200 | Derniers vestiges de linéaire B |
| 1200 à 750 | Disparition de la civilisation mycénienne des Achéens à l’arrivée des Doriens Importants mouvements migratoires : Béotie, Thessalie, Asie Mineure, Lesbos occupées par les Éoliens Corinthe, Péloponnèse, Crète, Rhodes occupés par les Doriens Attique, Eubée, Cyclades occupés par les Ioniens |
| 1100 | Destruction de Mycènes |
| 800 à 700 | Apparition de l’alphabet grec (origine phénicienne) et écriture de l’Iliade et de l’Odyssée par Homère. |
| 776 | Date retenue pour les premiers Jeux olympiques |
| 750 | Premières traces d’écriture en alphabet grec |
| 750 à 550 | Première période de colonisation grecque (Marseille, Asie Mineure, Mer noire) |
| 734 | Naxos, première colonie en Sicile |
| 733 | Les corinthiens fondent Syracuse en Sicile |
| ~700 | Hésiode écrit La Théogonie et Les Travaux et les Jours |
| 668 | Défaite de Sparte par les Argiens à Hysiae (Phidon est roi d’Argos) |
| 650 à 500 | Règne des tyrans à Athènes |
| 657 | Byzance (future Constantinople) colonie grecque est construite |
| 632 | La monarchie héréditaire est abolie par les nobles (eupadrides) et remplacée par un conseil de l’Aréopage. Ce conseil nomme des magistrats appelés archontes. Le peuple est doté d’une assemblée (ecclesia) qui ne peut qu’entériner les décisions des archontes. |
| 632 | Tentative de tyrannie populaire de Cylon |
| 621 | Dracon codifie les lois d’Athènes restées célèbres pour leur grande sévérité (" draconiennes ") |
| 595 à 590 | Première guerre sacrée concernant le sanctuaire de Delphes |
| 594 | Solon devient archonte et met en place une constitution qui remplace le privilège de la naissance par celui de la fortune. La société est remplacée en quatre classes censitaires selon le revenu. Le droit de vote et l’égalité de toutes les classes dans l’ecclésia sont reconnus. |
| ~594 | Solon met en place les mois caves et pleins |
| 585 | Thalès de Millet prédit une éclipse du soleil. |
| 582 | Les jeux Pythiques sont créés à Delphes et les jeux Isthmiques sont créés à Corinthe |
| 581 à 497 | Pythagore |
| 570 | Frappe de la première monnaie à Athènes |
| 561 | Première tyrannie de Pisistrate à Athènes |
| 549 à 546 | Conquête de la Médie et de la Lydie par Cyrus. |
| 546 à 527 | Dernière phase de la tyrannie de Pisistrate à Athènes |
| 546 | Sparte prédomine dans presque tout le Péloponnèse. Formation de la ligue du Péloponnèse. |
| 528 à 510 | Hipparque et Hippias, fils de Pisistrate gouvernent Athènes qui prospère |
| 525 | Conquête perse de l'Égypte |
| 521 | Darius s'empare du pouvoir en Perse |
| 514 | Hipparque, frère du despote Hippias est assassiné par Harmodius and Aristogiton |
| 513 | Darius envahit la Thrace |
| 510 | Hippias est renversé par les Spartes. Athènes devient une partie de la ligue du Péloponnèse |
| 508 à 506 | Archontat d'Isagoras. Réformes de Clysthène qui crée des institutions démocratiques |
| 499 | Révolte de l'Ionie contre la Perse |
| 498 | Athènes se joint à la révolte ionienne. Incendie de Sarde. |
| 494 | Bataille de Ladès |
| 490 | Première expédition perse en Europe. Bataille de Marathon qui voit la victoire des Athéniens sur l'expédition |
| 488 | Ostracisme à Athènes |
| 480 | Invasion perse de la Grèce. Nombreuses batailles |
| 478 | Fondation de la ligue de Delos sous l'hégémonie d'Athènes pour chasser les Perses de la mer Égée |
| 460 | Cimon remporte une série de victoires, consolidant les positions de la ligue en mer Égée |
| 462 | Réformes démocratiques d'Ephiate à Athènes |
| 446 | Paix de Callias : fin de la guerre avec les Perses. La ligue de Delos devient empire athénien. |
| 443 à 429 | Athènes de Périclès qui dirige la confédération de Delos et domine les mers grecques |
| 433 (ou 432) | Découverte (?) du cycle de 19 ans par Méton |
| 431 à 404 | Guerre du Péloponnèse. Victoire de Sparte sur Athènes |
| 429 | Mort de Péricles |
| 404 à 371 | Reddition d'Athènes, paix avec Sparte, mais Athènes garde sa suprématie intellectuelle et artistique |
| 371 | Thèbes arrive à vaincre Sparte et étend son hégémonie en Grèce occidentale. |
| 359 à 336 | Philippe II de Macédoine étend sa domination sur les cités grecques. |
| 356 à 323 | Alexandre III le Grand, fils de Philippe II |
| 347 | Mort de Platon |
| 337 | Alexandre le Grand envoyé en exil avec ses amis |
| 336 | Retour d’Alexandre après l’assassinat de Philippe II et déclaré roi. |
| 335 | Aristote part pour Athènes où il fonde une école |
| 334 à 330 | Alexandre le Grand conquiert l’Empire perse |
| 331 | Calippe de Cyzique, élève d'Eudoxe met au point les *calippiques* en créant une période de 76 ans |
| 331 | Alexandre fonde Alexandrie |
| 327 | L’armée d’Alexandre atteint les Indes. |
| 11 juin 323 | Mort d’Alexandre le Grand |
| .... | .... |
| ~160 ~120 | Hipparque de Nicée modifie la période calippique |
Le(s) calendrier(s)
| Auteurs des sources | Ère | Rôle |
|---|---|---|
| Hésiode | VIIIe - VIIe av. J.-C. | Poète grec |
| Aristoxène de Tarente | IVe av. J.-C. | Philosophe et musicien grec |
| Géminus ou Géminos | milieu du Ier siècle av. J.-C. | Auteur grec |
| Plutarque | env. 46 - env. 120 | Biographe et moraliste grec |
| Censorinus (Censorin) | env. 240 | Grammairien romain |
| Louis Ideler | 1766-1846 | Chronologiste allemand |
| Jean Chrétien Ferdinand Hoefer | 1811-1878 | Auteur d'ouvrages de l'histoire des sciences |
| M. De Koutorga | 1860 ? | Professeur à l'université de St. Pétersbourg |
Avertissement : Même si nous évoquons de temps à autre d'autres calendriers grecs, cette page est particulièrement consacrée au calendrier Attique et à son évolution. Une autre page sera consacrée au calendrier macédonien du fait de sa diffusion dans tout l'empire d'Alexandre. Nous ferons aussi le point sur les mois grecs autres que ceux d'Athènes dans une annexe.
Pourquoi ne pas traiter dans son ensemble le calendrier de la Grèce antique ?
Tout simplement parce que nous allons aborder, dans un premier temps, le calendrier des fêtes religieuses et que pratiquement chaque Cité grecque avait ses propres fêtes et, du coup, ses propres noms de mois et son propre début d'année.
Dès le IVe siècle av. J.-C. Aristoxène de Tarente, philosophe et musicien écrivait que "lorsque les Corinthiens en sont au dixième jour, les Athéniens n'en sont qu'au cinquième, d'autres en sont au huitième". Elem. harmon. Plutarque écrira plus tard :
Aristides §58 : Ils ont mené cette bataille le quatrième jour du mois Boedromion, selon les Athéniens, mais selon le Béotiens, le vingt-sept de Panemus ;[...] Il ne faut pas s'étonner de cette irrégularité dans les mois des Grecs, car encore de notre temps que la science de l'astronomie est plus cultivée et plus exactement approfondie, les uns commencent leurs mois lorsque les autres finissent les leurs.
Ceci étant précisé, entrons dans le vif du sujet.
À la recherche de la grande année
Je tiens à vous rappeler deux chiffres parce que nous allons courir après tout au long de cette étude sur les calendriers grecs :
Année tropique : 365,2421904 jours ; Lunaison : 29,5305882 jours.
Je dis nous, mais il ne faut pas croire pour autant que cette course était le passe-temps favori des Grecs de la période antique. C'était plutôt celui des astronomes de l'époque et leurs découvertes eurent peu ou prou (quand ce n'est pas aucune) d'incidence sur la vie quotidienne.
J'ai titré cette partie « à la recherche de la grande année ». Cette expression grande année, empruntée à Censorin (du jour natal XVIII) serait celle qui réconcilierait les mois lunaires et les années solaires. Dans une grande année de x années solaires, il y aurait un nombre entier de mois lunaires. Bref, à la recherche de la quadrature du cercle.
Laissons à Géminus (Introduction aux phénomènes célestes) le soin de nous expliquer la nécessité de construire un calendrier... luni-solaire (voilà qui est dit !) :
Les anciens se proposaient de régler les lois sur la Lune et les années sur le Soleil. Car les trois sortes de sacrifices que les lois et les oracles prescrivaient étaient, suivant les coutumes de leurs pères, ceux qui devaient se faire de mois en mois, ceux qui étaient fixés à de certains jours et ceux qui ne revenaient que chaque année. Tous les Grecs s'appliquèrent donc à faire accorder les années avec le Soleil, et les jours et les mois avec la Lune. On tâchait de faire accorder les années avec le Soleil, pour faire aux Dieux, toujours dans les mêmes saisons de l'année, les sacrifices prescrits, de sorte que celui qui devait se faire au printemps se fit effectivement dans le printemps; dans l'été celui de l'été [...]
Les Grecs se devaient donc de maintenir en phase année solaire et mois lunaires pour des motifs religieux.
Les calendriers agricoles
Et la vie quotidienne ? Et les tâches saisonnières de l'agriculture ?
Eh bien, pendant des siècles, des calendriers de la vie pratique (dits parapegmes) liant travail quotidien et événements astronomiques simples eurent un grand succès et se multiplièrent. Il est d'ailleurs étonnant que des savants réputés (Méton, Eudoxe, Calippe, Hiparque...) y collaborassent puisqu'il s'agissait de calendriers plutôt solaires alors que dans le même temps ils s'échinaient à accorder les deux chiffres cités plus haut pour en arriver à un calendrier luni-solaire très strict.
Ces calendriers parapegmes changeaient d'une Cité à l'autre et vivaient leur vie sans aucune coordination. Voici à quoi ressemblait un tel calendrier pratique tel qu'il était écrit par Hésiode dans Les travaux et les jours (VIIe siècle avant notre ère) :
Lever matinal des Pléiades. Les limaçons se montrent ; on aiguise les faucilles et la moisson commence.
Lever matinal du Baudrier d'Orion. On bat la moisson.
On voit Sirius le matin. Les chardons croissent, les cigales chantent.
Cinquante jours après le solstice d'été commence le second été. Sirius se voit pendant une partie de la nuit. Le temps est bon pour naviguer. Il y a de la chaleur humide et nuisible.
Lever matinal d'Arctutus. On prépare le vendange.
Si, à défaut de savoir repérer les Pléiades dans le ciel, vous êtes un spécialiste de la première apparition annuelle des limaçons ou du chant des cigales, vous pourrez mettre une date devant chaque événement. Je vous mets sur la piste : la première ligne correspond au 17 mai de notre calendrier.
Voir ici l'étude complète consacrée au calendrier d'Hésiode.
Essayons maintenant de suivre l'évolution de la précision de la grande année et donc celle des différents calendriers luni-solaires que connurent les Grecs dont les premiers se perdent dans la nuit des temps.
Les calendriers luni-solaires
1) Un calendrier lunaire de 354 jours
Hoefer (Histoire de l'astronomie) et Ideler (Historische Untersuchungen über die astronomischen Beobachtungen der Alten) s'accordent à dire que les premiers calendriers grecs furent essentiellement lunaires. Le mois débutait à la nouménie qui était l'instant ou la Lune, sous forme de croissant, commençait à devenir visible après la conjonction Soleil/Lune (nouvelle lune). Il se terminait à la nouménie suivante. De ce fait, la Pleine Lune occupait le milieu du mois ce qui lui valut le nom de dichoménie.
Cette année lunaire de 354 jours devait donc certainement comporter des mois de 29 et 30 jours qui furent appelés (à l'époque ou plus tard ?) respectivement creux et pleins.
2) Un calendrier luni-solaire avec des mois de 30 jours
Plus tard, on ne sait trop quand, mais déjà du temps d'Hésiode en tous cas, les Grecs donnèrent 30 jours aux 12 mois de l'année.
Et ils commencèrent à intercaler. Le pas était franchi et le calendrier luni-solaire était en train de naître.
Lisons ce qu'écrit Censorin à ce sujet :
"Plusieurs anciennes cités de la Grèce, ayant remarqué que, pendant l'année qu'emploie le soleil à accomplir sa révolution, il y avait quelquefois treize levers de la lune, et que cela arrivait une fois tous les deux ans, ont pensé qu'à l'année solaire répondaient douze mois lunaires et demi ; elles établirent donc leurs années civiles de manière à ce que, par une intercalation, les unes se composassent de douze mois et les autres de treize, appelant année solaire chacune d'elles prise isolément, et grande année la réunion de deux année solaires. Et cet espace de temps était appelé triétéride, parce que l'intercalation d'un mois avait lieu chaque troisième année, bien que cette révolution n'embrassât que deux ans, et ne fût en réalité qu'une diétéride"
Quelques commentaires sur ce texte :
- Plusieurs anciennes cités de la Grèce : Dit autrement et en ajoutant ce qu'on sait par ailleurs chaque Cité-Etat avait ses propres noms de mois basés sur des noms de fêtes ou de dieux associés à ces fêtes, commençait l'année un mois ou un autre et plaçait les mois embolismiques à sa guise l'une ou l'autre année.
- La période triennale était en fait biennale, mais l'intercalation se faisait après deux ans révolus comme si c'était dans la troisième année.
Avec cette période biennale, l'écart par rapport au Soleil était théoriquement de (360 X 24 + 30) - (365,25 X 2) soit 19 1/2 jour et de (360 X 24 + 30) - (29,53 X 25) par rapport à la Lune soit 11 3/4 jour .
À ce sujet, Ideler fait une remarque intéressante. Il note un passage de Cicéron qui précise que "Les Siciliens et les autres Grecs ont pour coutume de vouloir que leurs jours et leurs mois s'accordent avec le Soleil et la Lune ; en sorte que quelquefois, s'il y a une différence, ils retranchent du mois un jour, qui est le dernier ou deux ; Ils les appellent jours soustractifs, et d'autre fois aussi ils allongent le mois d'un ou de deux jours".
Ideler en conclut donc, qu'outre les mois intercalaires, les Grecs procédaient à des corrections ponctuelles pour que les mois restent toujours en phase avec la Lune. Il est fort probable qu'ils procédèrent ainsi dans les calendriers « améliorés » qui suivirent.
Geminus confirme cette supposition : "Une preuve que c'est avec raison que les jours du mois se comptent par la Lune, c'est que les éclipses du Soleil arrivent le dernier jour du mois où la conjonction se fait ; et les éclipses de Lune, dans la nuit d'avant le milieu du mois ; car alors la Lune est opposée au Soleil et entre dans l'ombre de la Terre."
3) Un calendrier luni-solaire avec des mois de longueur variable
Nous arrivons à l'époque de Solon vers 600 av. J.-C. Il trouve que le mois ne compte pas 30 jours et on peut raisonnablement penser que ce fut lui qui alterna les jours pleins de 30 jours et creux de 29 jours. Il introduit les dénominations d'ancien et de nouveau comme on peut en avoir une preuve sous la plume de Plutarque : "Solon avait observé l'inégalité des mois ; il avait vu que le mouvement de la Lune ne s'accordait ni avec le lever ni avec le coucher du Soleil ; que souvent en un même jour elle l'atteignait et le devançait. Il régla que ce jour serait appelé ancien et nouveau : il attribua au mois qui finissait la partie du jour qui précédait la conjonction ; et la partie qui la suivait, au mois commençant. [...] Solon appela le jour suivant néoménie."
En gardant le mois embolismique de 30 jours, cette alternance des mois de 30 et 29 jours fit que la période de 2 ans fut raccourcie de 12 jours. L'écart par rapport à la Lune passa à 6 heures environ et à 7 1/2 jours (trop longue) par rapport au Soleil. Il fallait donc oublier un mois intercalaire de temps à autre.
4) Une période de quatre ans ?
Si l'on en croit Censorin, la période de deux ans (appelée triennale) aurait été suivie par une période quadriennale (appelée quinquennale). Geminus n'en parle pas, mais Censorin écrit : "Ayant plus tard reconnu leur erreur, les anciens ont doublé cet espace de temps, et établi la tétraétéride, qui, parce qu'elle revenait à chaque cinquième année, fut nommée pentaétéride. Cette formation de la grande année par la réunion de quatre années solaires parut plus commode ; car, l'année solaire se composant de trois cent soixante-cinq jours et un quart environ, cette fraction permettait d'ajouter, tous les quatre ans, un jour plein à la quatrième année."
Comment était construite cette période de 4 ans si elle a existé ? Mystère.
5) Naissance de l'octaëtéride
Vers 450 av. J.-C. un astronome appelé Cléostraste de Ténédos proposa un système d'intercalation sur 8 ans, d'où son nom de cycle octaétéride. Ce système fut réellement adopté par les Grecs et employé couramment. Geminus le décrit ainsi :
Les anciens s'étant bientôt convaincus par les apparences du Soleil et de la Lune, que dans la trétéride les jours et les mois ne s'accordaient pas avec la Lune, ni les années avec le Soleil ; ils cherchèrent une période qui eut cette propriété, et qui contint des jours, des mois et des ans entiers. D'abord, ils formèrent la période de 8 ans (octaëtéride) composée de 99 mois, dont trois sont intercalaires, et qui contient 2922 jours. Voici comment ils disposèrent cette période : l'année solaire étant de 365,25 jours, et l'année lunaire de 354, on prit l'excès du premier de ces deux nombres, c'est-à-dire 11,25 jours huit fois, et l'on eut 90 jours ou trois mois de 30 jours chacun, et en les intercalant dans le cours de 8 années, les fêtes revinrent à leur propre saison. Ces mois intercalaires furent insérés après la 3e, la 5e et la 8eannée, et les autres mois furent comptés alternativement de 29 et 30 jours.
Censorin, lui, sur le même sujet, écrit :
[qu']on établit l'octaétéride, qu'on appela ennéaétéride, parce qu'elle reparaissait chaque neuvième année ; et cet espace de temps fut considéré, par presque toute la Grèce, comme la véritable grande année, parce qu'elle résulte d'un nombre d'années naturelles sans fraction, comme cela doit avoir lieu pour toute grande année. Celle-ci, en effet, se composait de quatre-vingt-dix-neuf jours pleins et huit années naturelles aussi sans fraction. L'institution de cette octaétéride est généralement attribuée à Eudoxe de Cnide; mais c'est à Cléostrate de Ténédos qu'appartient, dit-on, l'honneur de l'avoir inventée. Ainsi ont fait Harpalus, Nautélès, Mnésistrate, et d'autres encore, parmi lesquels Dosithée, dont le travail a pour titre : l'Octaétéride d'Eudoxe.
Geminus nous en apprend plus que Censorin sur la structure de cette période. En revanche, Censorin nous confirme l'intérêt que lui accordèrent les Grecs et nous donne le nom de son inventeur.
À propos des intercalations, Macrobe (Saturnales XIII) avance que "Ils [les Grecs] intercalèrent donc, chaque huitième année, quatre-vingt-dix jours, qu'ils divisèrent en trois mois de trente jours chacun. "
Bien entendu, il faut entendre « à la fin de la 8eannée » l'expression « chaque huitième année ». Qui de Geminus ou de Macrobe a raison ? Quand on sait quelle importance les Grecs apportaient au respect du début des mois, on ne peut qu'être étonné qu'ils aient pu attendre la fin de la période de 8 ans pour intercaler. C'est donc certainement Geminus qui a raison.
Nous n'avons pas manqué de noter le « d'abord » dans le texte de Geminus. En effet, il évoque à la suite de l'octaétéride une période de 16 ans (198 mois ou 5847 jours) et une période de 160 ans (58 440 jours en 1 979 mois). On se sait rien de ces périodes (date de découverte, auteur) et encore moins si elles furent d'usage dans la vie civile.
Il n'en reste pas moins vrai que la période de huit ans dura longtemps si on considère que le cycle de Méton que nous allons voir ne commencerait à être utilisé qu'à partir de 342 av. J.-C. environ. La trace la plus visible de ce cycle octaétéride se retrouve dans la durée des jeux olympiques de 4 ans qui correspondent à 1/2 cycle octaétéride.
6) Naissance de l'enneadécatéride (cycle de Méton)
433 av. J.-C. voit naître un nouveau cycle bien connu : le cycle de Méton ou cycle de 19 ans ou cycle enneadécatéride.
Méton d'Athènes, géomètre au siècle de Périclès serait à l'origine de ce cycle qui porte son nom. Je dis serait parce que si on va faire un tour du côté du calendrier babylonien on constate la connaissance d'un tel cycle depuis le VIIIe siècle avant notre ère. Pour en savoir plus sur le sujet et sur le personnage voir ici.
Le cycle de Méton répartit 6 940 jours sur 19 ans. Ils sont distribués en 235 mois dont 125 sont pleins et 110 caves.
Et là, nous n'allons pas manquer de lire ce qu'écrit Ideler parce que, à ma connaissance, c'est toujours d'actualité :
Pour pouvoir construire la période complètement, il fallait savoir sur quelles années les mois intercalaires devaient être distribués, ou quelles années de la période étaient composées de 13 mois. [...] Mais comme à cet égard nous manquons de tout témoignage bien clair de quelque ancien auteur qui pourrait seul décider la question, nous ne sommes pas en état de rétablir avec certitude le canon des 19 années de Méton. On ne peut pas même fixer au juste l'époque de sa période, quelle que soit la suffisance avec laquelle les chronologistes ont prononcé sur cet article.
Nous allons donc nous en tenir à des hypothèses. Le principe du cycle est le suivant :
- une constatation que 19 années solaires valent 235 lunaisons.
- Nous allons distribuer ces 235 lunaisons en 12 années de 12 mois lunaires et 7 années de 13 mois lunaires.
- 12 lunaisons font 354,367 jours. Nous aurons donc des années de 354 et 355 jours
- 13 lunaisons font 38,897 jours. Nous aurons donc des années de 383 et 384 jours.
Et nous en arrivons au tableau suivant :
| Nombre d'années | Nombre de jours | Jours |
|---|---|---|
| 5 | 355 | 1 775 |
| 7 | 354 | 2 478 |
| 6 | 384 | 2 304 |
| 1 | 383 | 383 |
| Total | 6 940 |
Les années embolismiques sont placées aux rangs 3 (ou 2), 5, 8, 11 (ou 10), 13, 16 et 19 (ou 18)... peut-être.
La valeur moyenne de l'année est de 3640/19 = 365,263 158 et celle du mois de 6940/235=29,531 915
Selon Diodore, le cycle aurait commencé le 13 Scirophorion (28 juin) dans la quatrième année de la 86e olympiade (433 av. J.-C.). Ideler nous fait remarquer à ce sujet "que les paroles de Diodore ne signifient certainement rien, sinon que Méton a commencé son calendrier astronomique* de 19 ans, mais non sa période, au 13 Scirophorion, jour du solstice d'été."
* ce « calendrier astronomique » était une éphéméride avant la lettre (ou un parapegme après la lettre) qui mentionnait les solstices, les levers et couchers des astres fixes et les températures habituelles. Il couvrait la période de 19 ans avec peut-être un peu de « rab » à ses extrêmes.
7) Perfectionnements ultérieurs
En 330, l'astronome Calippe y va de son cycle (qui ne sera, semble-t-il, pas appliqué dans la vie quotidienne) pour corriger l'erreur du cycle de Méton : il suggère de grouper 4 cycles de Méton en un cycle calippique de 76 ans et en supprimant un jour sur cette période.
Le cycle calippique comporte donc 27 759 jours. La moyenne de l'année est de 365,25 jours et celle du mois de 29,530 851 jours.
Cette période aurait été accueillie favorablement par les astronomes grecs. Son origine a été fixée au 28 juin 330 avant notre ère.
C'est en 130 av. J.-C. que l'astronome et mathématicien Hipparque est le premier à constater que l'année tropique n'est pas de 365,25 jours. Il fixe sa longueur à 365,246 528 jours (six minutes de trop) et celle de la lunaison à 29,530 579 jours (il manque une seconde). Pour corriger le calendrier, il propose d'enlever 1 jour chaque 4 cycles de Calippe (tous les 304 ans).
Avec Hipparque, on est arrivé à ce qui se fait de mieux dans la coordination des cycles solaires et lunaires. Je vous laisse quand même imaginer les dérives qu'il peut y avoir au cours de 19 ans (dans le cycle de Méton) et avant que tout ne rentre dans l'ordre.
Pour résumer, voici un tableau des différents cycles que nous avons évoqués :
| Année (av. J.-C.) | Nom | Jours | Années | Erreur | Lunaisons | Erreur |
|---|---|---|---|---|---|---|
| ? | - | 354 | 1 | 11,2 j | 12 | - 44 m. |
| ~600 | - | 738 | 2 | 3,8 j | 25 | - 15 m. |
| ~500 | - | 1 092 | 3 | 1,25 j | 37 | 24,6 m. |
| ~450 | Cléostrate | 2 922 | 8 | 11 m. | 99 | - 22 m. |
| 433 | Méton | 6 940 | 19 | 30 m. | 235 | 2 m. |
| 330 | Calippe | 27 759 | 76 | 11 m. | 940 | 22 s. |
| 143 | Hipparque | 111 035 | 304 | 6 m. | 3760 | - 0.4 s. |
Plus tard, après la réforme de César, les Grecs adoptèrent peu à peu le calendrier julien en gardant d'abord leur date de commencement de l'année et, en général, les noms de leurs mois. Commencement de l'année ? Mois ? parlons-en.
Les mois dans l'année
Voici un tableau des noms des mois dans différents États ou Cités puisque chaque Cité-État avait ses propres noms de mois basés sur des noms de fêtes ou de dieux associés à ces fêtes.
Nous essayerons plus loin d'y voir un peu plus clair dans les débuts d'année à Athènes. En attendant, nous nous contenterons de considérer cette liste comme une suite sans considérer le mois d'Hécatombéon comme étant le premier.
| Athènes | Macédoine | Delphes |
|---|---|---|
| Hécatombéon | Dios | Apellaeus |
| Metagitnion | Apellaios | Bucatius |
| Boédromion | Audynaios | Boathous |
| Pyanepsion | Peritios | Heraeus |
| Mœmactérion | Dystros | Daedaphorius |
| Posidéon | Xanthikos | Proetropius |
| Gamélion | Artemisios | Amlius |
| Anthestérion | Daisios | Bysius |
| Elaphébolion | Panemos | Theuxenius |
| Munychion | Loios | Endyspaetropius |
| Thagélion | Gorpiaios | Hericlius |
| Scirophorion | Hyperberetaios | Ilaeus |
Nous avons vu que le calendrier fit rapidement alterner les mois pleins de 30 jours et les mois caves de 29 jours. De plus, faire correspondre les mois attiques à nos mois grégoriens est risqué puisque des mois intercalaires étaient ajoutés.
Risquons-nous quand même et considérons le tableau qui suit avec beaucoup de réserves.
| Saison | Mois | Nbre jours | Grégorien |
|---|---|---|---|
| Été | Hécatombéon | 30 | Juillet-Août |
| Metagitnion | 29 | Août-Septembre | |
| Boédromion | 30 | Septembre-Octobre | |
| Automne | Pyanepsion | 30 | Octobre-Novembre |
| Mœmactérion | 29 | Novembre-Décembre | |
| Posidéon * | 29 | Décembre-Janvier | |
| Hiver | Gamélion | 30 | Janvier-Février |
| Anthestérion | 29 | Février-Mars | |
| Elaphébolion | 30 | Mars-Avril | |
| Printemps | Munychion | 29 | Avril-Mai |
| Thagélion | 30 | Mai- Juin | |
| Scirophorion | 29 | Juin-Juillet |
* A Athènes, le mois embolismique était placé après Posidéon et était appelé Posidéon II.
Les noms des mois rappelaient des coutumes ou événements. Par exemple pour les mois athéniens :
| Nom | Nom grec | Signification |
|---|---|---|
| Hécatombéon |
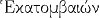
|
Sacrifice d'une hécatombe (100 bœufs) |
| Metagitnion |
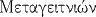
|
Mois des déménagements |
| Boédromion |
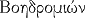
|
Célébration des Boédromies, en souvenir de la victoire de Thésée sur les Amazones |
| Pyanepsion |
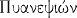
|
Fêtes en l'honneur d'Apollon, ainsi nommées parce qu'on mangeait ces jours-là des fèves cuites. |
| Mœmactérion |
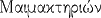
|
En l'honneur de Jupiter Mémactère (Dieu des tempêtes) |
| Posidéon |
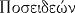
|
Fête de Neptune. |
| Gamélion |
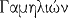
|
Mois des mariages. |
| Anthestérion |
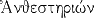
|
Fête en honneur des divinités infernales (époque du réveil de la nature) |
| Elaphébolion |
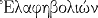
|
Fête de la chasse au cerf, en l'honneur de la déesse Artémis. |
| Munychion |
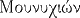
|
Fête de Diane Munychie |
| Thargélion |
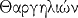
|
Fêtes en l'honneur d'Apollon et de Diane |
| Scirophorion |
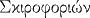
|
Mois des Scirophories, fêtes en l'honneur d'Athéna |
Le problème des mois Pyanepsion et Mœmactérion
Ces deux mois ont-ils été, à une époque ou une autre, inversés ? Telle est la question qu'on peut se poser et que quelques spécialistes se sont posés. Nous allons faire une « compil » des interrogations de Ideler et d'un certain Buttmann (professeur et bibliothécaire à Berlin, XIXe siècle) pour situer le problème.
Ideler note que Ptolémée mentionne les observations faites par l'astronome Timorachis dans la 283eannée av. J.-C. selon lesquelles il y aurait eu une occultation des pléïades (amas M45 dans la constellation du Taureau) au soir du 8 anthestérion et une occulation de l'épi (Spica dans la constellation de la Vierge) le 6 pyanepsion. Ces deux observations étaient séparées de 283 jours. Si pyanepsion avait été avant Mœmactérion, l'écart relevé aurait été trop grand de 29 ou 30 jours.
Buttmann avance d'autres arguments en faveur d'un ordre Mœmactérion-Pyanepsion. Voyons-en une pas trop technique :
Aristote (Hist. nat. L. VI), à propos du temps de rut des cerfs (je voulais dire pas trop technique... astronomique), explique que « leur accouplement se fait après arcturus, vers Boédromion et Mœmactérion ». Cette façon de s'exprimer veut en général dire X et Y et non pas DE X à Y.
Mais, ni Buttmann ni Ideler n'ignorent l'existence de deux inscriptions lapidaires relevées par un autre spécialiste, Corsini dont l'une dit : En Boédromion, Nymphodote. En Pyanepsion, Demetrius. En Mœmactérion, Sympheron.
Il s'agit d'inscriptions mentionnant le nom des préfets à Athènes au temps des empereurs.
Et Buttmann ne croit pas un instant "qu'aucun gouvernement ou particulier voudrait laisser subsister une inscription sur une pierre où on aurait marqué un mois pour un autre".
Il conclut l'ensemble de son analyse en reconnaissant le problème de l'ordre de ces deux mois, mais ne prend pas position.
Ideler, lui, pense que les deux mois n'avaient pas la même place à des époques différentes.
Le fait est qu'aucun auteur ancien n'a donné l'ordre des mois dans l'année. Le problème est posé. Je vous laisse le soin de vous faire votre propre opinion ou.... de creuser un peu mieux. Et si vous trouvez des éléments, merci de penser à moi en me les faisant connaître:-))
Le jour
Au temps de la Grèce archaïque, il commençait au coucher du soleil et était divisé en deux parties inégales, la partie diurne et la partie nocturne. Ces deux parties étaient elles-mêmes divisées en trois parties mal délimitées (début, milieu, fin).
La journée s'appelait nycthémère. Après Alexandre le Grand, on fit commencer le jour civil au lever du soleil. Vers 600 av. J.-C. les cadrans solaires font leur apparition, mais ce n'est que beaucoup plus tard (sous Alexandre). que la journée fut divisée en 2 groupes de 12 heures qui, d'ailleurs, variaient en longueur.
Le décompte des jours du mois
Comme nous l'avons vu plus haut, le mois était supposé commencer avec la noémenie mais le manque d'intercalations correctes le faisait dériver et des rattrapages étaient faits régulièrement.
Le mois était divisé en trois décades de 10 jours. Dans les mois caves, la dernière décade n'avait que 9 jours. Le premier jour du mois (premier jour de la première décade) était appelé néoménia et le dernier triacade. Dans les deux premières décades, on désignait les jours par leur rang dans la décade. Le décompte se faisait à l'envers dans la troisième décade. Ce qui donne le tableau ci-dessous.
| Décade du commencement | Décade du milieu | Décade d'avant la fin (mois plein) | Décade d'avant la fin (mois cave) |
|---|---|---|---|
| néoménia | premier | dixième | neuvième |
| deuxième | deuxième | neuvième | huitième |
| troisième | troisième | huitième | septième |
| quatrième | quatrième | septième | sixième |
| cinquième | cinquième | sixième | cinquième |
| sixième | sixième | cinquième | quatrième |
| septième | septième | quatrième | troisième |
| huitième | huitième | troisième | deuxième |
| neuvième | neuvième | deuxième | triacade |
| dixième | dixième | triacade |
Comme on peut le remarquer, le décompte des jours de la dernière décade ressemble à ce que pratiqueront les Romains avec le système de Calendes. Ce comput inversé apporte, selon moi, un élément au fait qu'on rattrapait (en dehors des mois embolismiques) régulièrement le retard entre le début de mois et la noéménie en ajoutant ou supprimant des jours comme l'a décrit Cicéron.
Le début de l'année
C'est dans le début d'un texte de De Koutorga (Recherches critiques sur l'histoire de la Grèce pendant la période des guerres médiques) qu'on peut trouver un point précis des connaissances sur le début de l'année. De plus De Koutorga y fait sa propre analyse du sujet.
Le chapitre 1 de la première partie commence ainsi :
"Dans la deuxième moitié du cinquième siècle avant Jésus-Christ, et nommément depuis la guerre du Péloponnèse, l’année athénienne commençait au mois d’hécatombéon. Le témoignage de Thucydide est positif à cet égard. En commençant, dans son deuxième livre, le récit de la guerre, il fixe avec une grande exactitude l’époque des premières hostilités. Il dit que les Thébains ouvrirent la guerre au printemps de la quinzième année après la conclusion du traité de trente ans, le sixième mois après la bataille de Potidée, lorsque Chrysis était prêtresse de Junon à Argos, Enesias éphore à Sparte, et Pythodore archonte à Athènes ; il ajoute que ce dernier n’avait plus que deux mois à rester en charge. On voit, par ce témoignage, que l’année athénienne finissait dans deux mois et qu’elle recommençait en été."
De Koutorga part du postulat (et donc, sans le démontrer) que l'année civile attique commençait en même temps que la prise en charge de leurs fonctions par les magistrats. Et donc, printemps + 2 mois = hécatombéon. Mouais...
Je signale au passage que toutes les traductions différentes du texte de Thucydide disent « quatre mois » et non pas deux. Et comme je ne lis pas le Grec, si quelqu'un pouvait vérifier et me dire ce qu'il en est exactement, je lui en serais reconnaissant.
De Koutorga fait ensuite un inventaire des différentes positions des chronologistes sur ce problème de début de l'année athénienne :
- Scaliger en tête, suivi par Petau, Dodwell, Corsini, Larcher, Ideler pensent que les Athéniens, primitivement, faisaient commencer l'année en hiver au mois gamélion.
Ce qui expliquerait que, posidéon se trouvant être le dernier mois de l'année, le mois intercalaire fut logiquement placé après ce mois et prit le nom de posidéon II. - Petau ajoute que le déplacement du début de l'année de gamélion à hécatombéon fut en fait un retour à une situation antérieure où ce mois était déjà le premier de l'année. Les Athéniens auraient donc dans un premier temps fait commencer l'année en été (hécatombéon), puis en hiver (gamélion) et, enfin à nouveau en été (hécatombéon).
- D'autres, au contraire, comme Fréret et Clinton, pensent que l'année athénienne aurait toujours commencé en été.
De Koutorga se lance alors dans des recherches pour tenter de savoir qui des uns ou des autres à raison.
Pour ma part, je retiens de ces recherches que pas un auteur ancien ne dit « l'année commençait au mois de XXXX ». Alors, il ne reste plus qu'à interpréter des phrases de ces auteurs pour essayer de leur faire dire quelque chose. Prenons un exemple détaillé par De Koutorga
"[...] Hérodote indique d’une manière aussi précise le commencement de l’année athénienne. Il raconte dans son VIe livre les mouvements de la flotte phénicienne pendant toute la bonne saison, c’est-à-dire du printemps à l’automne. Il décrit la prise des îles de l’Hellespont, de Byzance, mentionne la fuite de Miltiade en Attique, et, après avoir conduit son récit jusqu’en automne, il ajoute [VI, XLII] : « Dans le reste de cette année, les Ioniens n’eurent rien à souffrir des Perses. » Quand donc peut-on penser que l’année se termina ? Nous croyons que par ces mots, « le reste de l’année, » Hérodote ne pouvait désigner que l’hiver. Mais lui-même se charge un peu plus loin de fournir la réponse. "Avec le printemps suivant, dit-il [VI, XLIII], Mardonius, fils de Gobryas, arriva à la mer à la tête de grandes forces." On voit par ces deux passages qu’une année avait fini après l’automne ; qu’une autre avait recommencé avant le printemps, c’est-à-dire en hiver."
Oui, mais on peut aussi lire : "La flotte des Perses, qui avait passé l'hiver aux environs de Milet, ayant remis à la voile la seconde année, prit aisément les îles voisines du continent [...]".
Suite à de nombreuses interprétations de ce genre, De Koutorga en arrive à la conclusion suivante : "En résumé, les preuves exposées ci-dessus renversent l’opinion de Fréret et de Clinton, et donnent à l’hypothèse de Scaliger la valeur d’une vérité historique.".
L'année attique aurait donc commencé en hiver, puis en été.
Et il se pose la question du quand. "Pour compléter notre travail, passons maintenant à une autre question, intimement liée à celle-ci, et cherchons à quelle époque les Athéniens ont transporté le commencement de l’année de l’hiver à l’été."
Là aussi, il va être catégorique :
Dodwell, Corsini, Larcher, et la plupart des chronologistes qui acceptent le mois de gamélion comme le premier de l’année, ont pensé que cet usage a duré jusqu’au commencement de la 87e olympiade, et ne fut changé que par Méton, qui introduisit le cycle de dix-neuf ans. Nous partageons cette opinion, car elle est fondée sur un témoignage positif, celui de Festus Avienus, dans les vers duquel se trouve la description la plus exacte du changement opéré par l’astronome Méton. Il est vrai qu’Ideler repousse le témoignage de Festus, en la qualifiant d’idée de poète. Mais il a tort ; ces vers n’ont que la forme de poétique, ils contiennent une description très précise, que nous chercherions inutilement chez d’autres écrivains.
Nam qui solem hiberna novem putat æthere volvi,
Ut lunæ spatium redeat, vetus Harpalus, ipsam
Ocius in sedes momentaque prisca reducit.
Illius ad numeros prolixa decennia rursum
Adjecisse Meton Cecropia dicitur arte ;
Inseditque animis, tenuit rem Græcia solers,
Protinus, et longos inventum misit in annos.
Sed primæva Meton exordia sumpsit ab anno,
Torreret rutilo quum Phœbus sidere Cancrum, etc.En voyant ce témoignage, on a une preuve de plus qu’à l’époque des guerres médiques les Athéniens commencèrent leur année civile en hiver, et on ne saurait douter que le changement n’ait été effectué par le gouvernement de la république, sur la proposition de Méton.
La traduction (ici sur le site de Philippe Remacle, François-Dominique Fournier, J. P. Murcia et Thierry Vebr) des vers de Festus est la suivante :
Par exemple, l'antique Harpalus, qui pense qu'il faut que le Soleil
roule pendant neuf hivers pour que la Lune retrouve son point de départ,
la ramène trop tôt à son berceau : À ce nombre, on rapporte que le
savant Athénien Méton ajouta dix longues années ; ce système prévalut :
la docte Grèce l'adopta et le transmit pour longtemps à la postérité,
Toutefois Méton a placé le commencement de l'année au moment où Phébus
brûle le Cancer des feux de son astre où la ceinture d'Orion flotte au
loin sur la mer, et où le Sirius lance les flammes de ses étoiles sombres.
Ne nous cassons pas la tête, le Cancer brûlé par Phébus, c'est en été. Ce qui est intéressant c'est le « Toutefois » (ou « Mais »). Ideler qui, contrairement à ce que dit De Koutarga, ne repousse pas ce texte, écrit "Le mot ,mais montre qu'effectivement on a changé la saison du commencement de l'année. Quoiqu'il en soit, il est prouvé au moins, par plus d'un endroit de Thucydide, de Platon et de Démosthène, qu'aux temps de ces auteurs, l'année commençait vers le solstice d'été".
Pour ma part, je me pose la question suivante : « Toutefois (ou, Mais) par rapport à quoi ? ». Et si c'était simplement un problème « scientifique » de début de cycle sans grand rapport avec l'année civile des Athéniens ?
Un début d'année au mois hécatombéon, c'est certain. Un début d'année au mois gamélion dans les périodes précédentes expliquerait la position du mois complémentaire. Le débat est loin d'être clos. N'hésitons pas à y ajouter une question que De Koutarga ne s'est pas posée, celle du pourquoi un changement ? Pour accorder le début de l'année et les olympiades ?
Chronologie grecque
Jusqu'au troisième siècle avant notre ère, il n'y eut pas de véritable chronologie puisque chaque Cité faisait comme bon lui semblait. Les Athéniens associaient les années à la magistrature de l'archonte éponyme qui siégeait. Les Spartiates, eux, faisaient référence au président du collège des Ephores...
Après Alexandre, les Grecs comptèrent les années par référence aux Olympiades. Le point de départ de cette ère fut fixé à la date des premiers Jeux olympiques soit à l'année 776 av. J.-C. L'indication se faisant avec deux chiffres : le premier était celui de l'olympiade et le second le rang de l'année dans celle-ci. Par exemple la seconde année des 100e olympiades était notée Ol. 100,2.
Il existait aussi à Athènes une autre référence qui était une « chronologie politique ». Après la réforme de Clisthène (fin du VIe siècle avant J.-C.) la Grèce est divisée en 10 tribus. 50 membres (bouleutes) de chaque tribu composent un conseil de 500 membres (la Boulé). Pour régler les affaires courantes, seuls 50 bouleutes d'une tribu effectuent une « permanence » suivant un ordre défini par le sort (bureau exécutif de la Boulé). Cette permanence est assurée pendant un dixième de l'année. L'année athénienne était donc divisée en 10 prytanies d'une durée de 36 ou 39 jours (elle passera plus tard à 30 jours). Les documents administratifs étaient datés du nom de la tribu « de permanence » et du jour de la prytanie.
Enfin, l'astronome grec Ptolémée, au IIe siècle apr. J.-C. inventa de toutes pièces une ère artificielle pour tirer parti des observations des babyloniens : L'ère de Nabonassar dont le point de départ était le 26 février 747 av. J.-C. Elle ne fut utilisée que par les astronomes et les historiens.
Note
La Grèce est passée au calendrier grégorien en 1920.
La règle de division par 400 a été modifiée ainsi : toute année divisible par 900 dont le reste est 200 ou 600 est une année bissextile. Cette règle donne 218 années bissextiles tous les 900 ans ce qui donne une moyenne annuelle de 365,24222 jours plus proche de l'année tropique que l'année moyenne du calendrier grégorien (365,2425 jours).