- Accueil
- À ne pas manquer
- Calendriers Saga
- Études thématiques
- Méton et le cycle de 19 ans
Avant de nous demander si Méton a vraiment découvert le « cycle de Méton », nous allons essayer de savoir qui était réellement Méton et ce qu'il a précisément découvert.
Qui était Méton ?
On se sait pratiquement rien de Méton sinon qu'il était natif de Leuconoé, canton de l'Attique, proche d'Athènes. Elien, auteur de la première moitié du 3èmesiècle après J.-C, dans ses Histoires diverses écrit "Méton de Leuconée, autre astronome, fit élever des colonnes sur lesquelles il marqua les révolutions du soleil, et se vanta d'avoir trouvé la grande année, qu'il assurait être de dix-neuf ans."
L'auteur comique Phrynichos, contemporain d'Aristophane, dans sa pièce Monotropos, situera aussi la naissance de Méton à Leuconoé.
On sait aussi qu'il vécu dans la seconde moitié du cinquième siècle avant J.-C.
Elien, au 3èmesiècle, le présente comme étant astronome. Et, de nos jours, on le considère comme tel.
Il semble pourtant bien que cette réputation d'astronome ne fut que posthume et que de son vivant il était plutôt connu comme géomètre.
Puisque nous avons évoqué Aristophane, lisons un passage de sa pièce Les Oiseaux dont il est l'auteur et qui fut jouée en 414 av. J.-C. Aristophane introduit Méton lui-même dans la pièce comme personnage.
METON : Je viens auprès de vous.
PISTHETAEROS : Autres facheux ! Que viens-tu faire ici ? Quel est ton dessein ? l'idée de ton voyage ? ta démarche de porteur de kothurne ?
METON : Je veux toiser l'air et vous le partager en rues.
PISTHETAEROS : Au nom des dieux, quel homme es-tu ?
METON : Qui je suis ? Méton qui connaissait la Hellas et Kolônos.
PISTHETAEROS : Dis-moi, qu'est-ce que tu as avec toi ?
METON : Des mesures de l'air. Sache, en effet, tout d'abord, que l'air dans son entier est absolument semblable à un four. À l'aide de cette règle courbe, tombant d'en haut, et en y ajustant le compas... Comprends-tu ?
PISTHETAEROS : Je n'y comprends rien.
METON : J'applique une règle droite, de manière à ce que tu aies un cercle tétragone ; au centre est l'Agora, les rues qui y conduisent sont droites et convergentes au centre, ainsi que d'un astre, qui est rond de sa nature, partent des rayons droits qui brillent dans tous les sens.[....]
PISTHETAEROS : Ne l'avais-je pas dit depuis longtemps ? Va-t-en prendre tes mesures ailleurs.
Dans ce passage, Méton est présenté comme géomètre et non comme astronome. Un géomètre qui prétendrait donner une solution au problème de la quadrature du cercle.
Et pourquoi connaissait-il particulièrement Kolônos (Colone non loin d'Athènes) ? Les uns ont avancé que c'est parce qu'il y était né, d'autres parce qu'il y avait construit une fontaine ou un aqueduc. Dans le Monotropos dont nous avons déjà parlé, Phrynichos écrit : « Méton de Leuconoé, celui qui amène les sources ».
Pourtant, Philochore, auteur du 3èmesiècle av. J.-C. précise que Méton n'a jamais rien construit à Colone mais qu'il avait élevé en 432 un héliotropion (gnomon avec repères des solstices) « dans l'endroit où se tient maintenant l'assemblée, près du mur du Pnyx ».
Le Pnyx, installé sur une colline faisant face à celle de l'Acropole, était le lieu de rassemblement des Athéniens qui y tenaient assemblée. C'est là que Méton aurait érigé son héliotropion... ou autre chose... ou rien.
Une dernière anecdote sur Méton nous est encore rapportée par Elien dans ses Histoires diverses - LIVRE XIII
12. De l'astronome Méton.
LORSQUE la flotte d'Athènes fut prête à faire voile vers la Sicile*, l'astronome Méton, qu'on avait compris dans la liste de ceux qui devaient s'embarquer, prévoyant l'événement et craignant les dangers de la navigation cherchait à se dispenser du voyage. Comme il n'y réussissait pas, il prit le parti de contrefaire l'insensé : entre diverses extravagances qu'il crut propres à confirmer l'opinion qu'il l'était réellement, il mit le feu à sa maison, qui était dans le voisinage du Poecile : sur cela, les archontes lui donnèrent son congé. À mon avis, Méton joua mieux le fou que n'avait fait Ulysse, roi d'Ithaque. Palamède découvrit la ruse d'Ulysse, et aucun Athénien ne s'aperçut de celle de Méton. Justin, IV, 4.
* Les Athéniens portaient la guerre chez les Syracusains : cette expédition ruina les forces d’Athènes et fut suivie de la prise de cette ville par les Lacédémoniens.
Gardons nous bien d'en tirer une conclusion hâtive. Parce que d'autres textes avancent que c'est pour sauver son fils que Méton eut ce comportement. À moins que ce ne soit par conviction politique.
Ce paragraphe ne serait pas complet si nous ne parlions pas d'Euctémon, « collègue » de Méton et certainement coauteur du cycle qui nous intéresse. Ce sera vite dit puisqu'on ne sait rien de lui sinon qu'il était, lui, astronome.
Quel fut le rôle de l'un et de l'autre dans l'invention du « cycle de Méton » ou « grande année » ? En l'état actuel de nos connaissances, nous ne le savons pas.

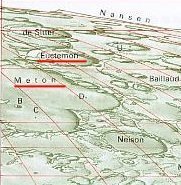
Certainement très proches dans la vie, Méton et Euctémon le sont aussi sur la Lune où deux cratères proches portent leurs noms.
Hasard ou volonté, le cratère Méton est dans l'obscurité jusqu'au 19èmejour à partir de la nouvelle Lune. À ce moment, il devient visible.
Qu'a-t-il découvert exactement ?
Qu'on l'appelle cycle de 19 ans, cycle métonique, année de Méton, grande année ou ennéadécatéride, peu importe, Méton et Eucténon inventèrent un cycle qui veut que
19 années solaires = 235 lunaisons
Telle quelle, cette égalité ne signifie pas grand chose si nous ne connaissons pas la durée d'une année solaire ou d'une lunaison.
Quelles étaient ces valeurs au temps de Méton ? Nous n'en savons pas grand chose. Mais, heureusement, nous savons que la durée du cycle était de 6940 jours.
Si le cycle était exact, cela nous donnerait une année solaire d'une durée de 365,26316 jours et une lunaison d'une durée de 29,5319 jours.
Nous savons qu'il n'en est rien puisque l'année tropique dure 365,242219 jours et la lunaison 29,53059 jours environ. Les deux durées étaient trop longues et firent l'objet de cycle plus longs et plus exacts. Mais c'est une autre histoire (voir à ce sujet la page sur les ères et cycles).
Ceci dit, rien ne permet de dire que les chiffres ci-dessus furent ceux utilisés ou découverts par Méton et Eucténon. On peut supposer que tout cycle donnant une durée totale proche de 6940 peut être valable.
Selon Bigourdan (1851/1932), astronome de métier, pour Méton « l'année vaut 365 jours 5/19 et la lunaison 29 jours 25/47 ». Pourquoi pas ? Cela nous donne un cycle de 6939,999 jours. Cela n'a, en fin de compte, guère d'importance.
Que signifie ce cycle et comment l'utiliser ?
Du strict point de vue astronomique, il signifie que, tous les 19 ans, la Lune revient exactement (oublions qu'il n'est pas exact) au même endroit dans le ciel. On vérifie ?
C'est facile de faire cette vérification avec nos logiciels modernes d'astronomie. Pour les images qui suivent, j'ai utilisé Alphacentaure. Mais j'aurais pu tout aussi bien me servir de Cartes du ciel. Ce sont deux logiels libres d'une exceptionnelle qualité. Ces hommages mérités étant rendus, revenons à nos.. Méton et Eucténon.
Prenons un lieu d'observation au hasard, Athènes par exemple. Prenons une date au hasard, le 28 juin 433 av. J.-C. dans le calendrier julien. Par exemple à 23 H 00.
Où est la Lune dans le ciel pour ce lieu et à cette date ?
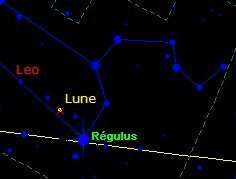
Où est la Lune pour le même lieu 6940 jours plus tard, soit un cycle de Méton plus tard.
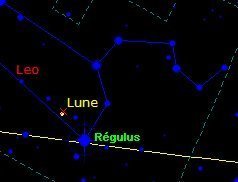
Elle est pratiquement au même endroit. Pour dire exactement, il aurait fallu qu'elle se situe au centre de la croix rouge qu'on distingue un peu au-dessus de sa position réelle. Cette différence de position matérialise l'erreur du cycle.
Je ne sais pas ce que vous auriez fait, vous, à l'œil nu et pratiquement sans aucun moyen moderne de pointage, mais, pour ma part, je trouve que c'est pas mal du tout.
On peut utiliser ce cycle à deux fins :
- Pour connaître à l'avance les phases de la Lune. Il suffit de les noter pour 19 ans. Ensuite, elles reviennent au même jour dans les cycles suivants. C'est exactement ce que fit Denys le Petit (vers 532) qui dressa la table des lunes « fictives » (ou ecclésiastique ou calendaire) dans le calendrier julien. Le cycle de Méton fera les beaux jours du calendrier ecclésiastique pendant des siècles. Pour en savoir plus, voir la page sur la calendrier ecclésiastique.
- Dans les calendriers luni-solaires pour savoir quelles années doivent être embolismiques (avec un 13èmemois) pour que l'année lunaire garde le contact avec l'année solaire.
Méton et Eucténon dressèrent-ils une telle table du rang des années embolismiques ? C'est fort probable puisque le but du cycle était quand même d'en finir avec la dérive du calendrier grec.
Les intercalations dans les années 3, 5, 8, 11, 13, 16, 19 et le nombre de jours de chaque mois de l'année sur lesquels nous ne reviendrons pas (tous les détails sont ici) ont-elles été fixées ainsi par Méton et Eucténon ? Nul ne le sait mais peu importe, c'est le principe qui compte : intercaler 7 mois complémentaires dans un cycle de 19 ans pour que le total des jours de ce cycle fasse bien 6940 jours.
Quand fut inventé le cycle et quelle était sa date de départ ?
Suivant Diodore, Méton aurait fait commencer son cycle le 13èmejour du mois Scirophorion dans la quatrième année de la 86ème Olympiade. Ce qui correspondrait au 28 juin 433 av. J.-C. (julien).
Pour sa part, Jean-Étienne Montucla (1725-1799), dans son histoire des mathématiques (1799), avance une autre date : "...Ce cycle fut établi en l'an 433 julien avant J.C., le 16 juillet, 19èmejour après le solstice d'été ; et la nouvelle lune qui arriva ce jour à sept heures 43 du soir, en fut le commencement, le premier jour de la période étant compté du coucher du soleil arrivé la veille. Méton choisit à dessein cette nouvelle lune, quoique plus éloignée du solstice que la précédente, afin de ne pas être obligé d'intercaler dès la première année. Car l'année grecque était telle que la pleine lune de son premier mois devait être postérieure au solstice, à cause des jeux olympiques dont la célébration était fixée au milieu de ce premier mois après le solstice d'été..."
Alors ? Diodore ou Montucla ?
Venons-en à la légende de l'histoire du cycle de Méton. Et Montucla va nous aider à entrer de plein pied dans le sujet. Il écrit que "...Méton exposa à Athènes, et probablement devant la Grèce assemblée à ces jeux célèbres, une table où l'ordre de sa période était expliqué, et l'applaudissement avec lequel elle fut reçue de la plupart des nations Grecques, lui fit donner le nom de cycle ou de nombre d'or..."
Pourquoi nombre d'or ? Parce que, parait-il cette table aurait été inscrite en lettre d'or sur des tablettes attachées aux monuments publics (Hoeffer, 1873). À moins que ce ne soit directement sur le mur du Pnyx ou sur le Temple de Minerve qui est je ne sais où.
Bref, on lit de tout à ce sujet. Et la réalité est beaucoup plus triste, surtout pour Méton...
Sa découverte est passée pratiquement inaperçue. Géminus, dans son introduction aux phénomènes ne cite même pas Méton et attribue la paternité du cycle à Callipe.
Le cycle ne fut pas appliqué en Grèce avant 342 ou 330 av. J.-C.
Ce qui fait qu'en 423 av. J.-C. Aristophane dans La Paix, se plaint toujours des désordres du calendrier :
"En venant ici, nous avons rencontré Diane (la Lune), [...] qui nous a dit qu'elle était fort en colère des injures qu'elle reçoit tous les jours. [...] Elle se plaignait de ce que vous n'observez pas du tout ses jours de fête, et de ce que vous les laissez aller confusément. [...] Et pendant que, nous autres dieux, nous célébrons des jeûnes, c'est justement ces jours-là que vous faites vos libations et vos banquets".
Comment Aristophane qui, comme on l'a vu, connaissait Méton aurait-il pu oublier une célébrité couronnée aux jeux olympiques et se plaindre encore du calendrier ?
Quant au fameux Nombre d'Or gravé un peu partout, il semble qu'il date de 1170, année où Alexandre de Villedieu écrit son Massa compoti. Et ce n'est qu'au 13èmesiècle qu'on peut lire sous la plume d'un 'savant« que »ce nombre dépasse tous les autres calculs lunaires comme l'or dépasse les autres métaux".
D'ailleurs, Denys le Petit, qui utilise le nombre d'or dans ses tables ne parle pas de nombre d'or mais de cyclus decemnovennalis.
A-t-il découvert « son » cycle ?
Nous allons oublier l'astronomie chinoise qui, selon les sources, aurait eu connaissance du cycle de 19 ans à des dates diverses et variées. Sans pour autant que les sources des informations soient claires. Ainsi, on peut lire que le cycle de 19 ans aurait été connu dès le 27 ème siècle avant J.-C. à la suite d'observations faites à l'observatoire construit par Hoang-Ti. D'autres avancent la dynastie Shang (1554-1145 av. J.-C.).
Retenons simplement ce qu'écrit Helmer Aslasken dont la connaissance du calendrier chinois n'est plus à démontrer. Selon lui, le cycle de Méton est connu en Chine sous le nom de cycle zhang depuis environ 600 av. J.-C. Les premiers calendriers utilisant ce cycle dateraient d'avant 104 av. J.-C.
En revanche, nous allons nous pencher sur le cycle de 19 ans chez les Babyloniens.
Remerciements
Avant de commencer, je voudrais juste remercier trois personnes :
Emmanuel Bertin pour avoir fait un énorme travail de « repérage » des mois complémentaires dans les textes babyloniens.
G.R.F. Assar pour ses conseils éclairés, sa patience et sa disponibilité. C'est grâce à lui que nous avons pu, Emmanuel et moi, corriger certaines erreurs de datation. Les constatations qui suivent rejoignent ses propres conclusions exprimées dans « Parthian Calendars at Babylon and Seleucia on the Tigris », IRAN 41 (2003), 171-185.
Et je m'en voudrais d'oublier de remercier aussi Francis Joannès. D'abord pour le site http://www.achemenet.com qui est une véritable mine pour ceux qui se penchent sur les textes babyloniens. Ensuite pour ses précieuses précisions sur la manière de « décoder » les dates babyloniennes et s'y retrouver dans la chronologie.
Le cycle de 19 ans et les Babyloniens
Pourquoi cette étude minutieuse des textes datés ? Tout simplement parce que la lecture de quelques livres donne une impression de flou et laisse la place au doute en ce qui concerne la datation de l'application du cycle de 19 ans par les Babyloniens.
Dans son livre La Mésopotamie (1985) Georges Roux écrit que "Les astronomes ayant remarqué que 235 mois lunaires faisaient exactement 19 années solaires, en 747 le roi Nabû-nâsir, à Babylone, décida l'introduction de sept mois supplémentaires étalés sur une période de 19 ans ; toutefois, ce "calendrier de Nabonassar« ne fut standardisé qu'entre 388 et 367 ». En ce qui concerne les dates, le texte renvoie à Babylonian Chronology 626 BC - AD 75. (1956) de Parker, Richard A. and Waldo H. Dubberstein.
Parker et Dubberstein écrivent dans ce livre : "In the fourth century - in 367 B.C according to our scheme - the intercalations became standardized, and the nineteen-year cycle came into being."
O. Neugebauer, lui, dans The exact sciences in antiquity fait remarquer que, selon A. Sachs, les règles d'intercalation ont été fixées antérieurement à 380 av. J.-C.
Antérieurement, oui, mais de combien d'années ? avant 433 ou après ? Qu'entend-on par « standardisation » ? Comment se présentait le calendrier avant cette standardisation ? C'est ce que nous avons essayé de savoir.
Rappels sur le calendrier babylonien
Pour l'époque qui nous intéresse, de Nabonassar à Alexandre le Grand, c'est-à-dire de 747 av. J.-C. à 330 av. J.-C. le calendrier est luni-solaire.
Les mois ont pour nom Nisanu, Ayaru, Simanu, Duzu, Abu, Ululu, Tashritu, Arahsamnu, Kislimu, Tebetu, Shabatu, Addaru.
Les mois intercalaires, quand il y en a, le seraient après Ululu ou Addaru et sont appelés tout simplement second Ululu ou second Addaru. Le cycle de 19 ans, quand il fut fixé, aurait intercalé dans les années 1, 3, 6, 9, 11, 14 et 17. On aurait intercalé un second Ululu dans l'année 1 du cycle et un second Addaru toutes les autres années.
Jusqu'à l'ère Séleucide, les années étaient comptées à partir de l'accession au trône d'un nouveau roi. Lorsque, dans la même année, un roi décédé était remplacé par un autre, il a été décidé par convention de compter la dernière année de règne du roi défunt comme une année pleine, et d'appeler « année inaugurale » (ou« année 0 ») la période de quelques mois servant à terminer la dernière année officielle de ce roi. À l'ère Séleucide le compte devint continu et l'année 1 de l'ère Séleucide correspond à 312/311 av. J.-C.
Résultat de la compilation des textes datés
Pour ne pas avoir à étudier un tableau trop long, nous allons le raccourcir pour nous en tenir seulement à sa partie intéressante et significative.
Nous noterons A l'année contenant un second Addaru et U l'année contenant un second Ullulu.
| Roi | Dates de règne | Année de règne | Mois intercalaires | Cycle |
|---|---|---|---|---|
| Nabonide | 555/554 | 1 | A | Aucun. Les mois complémentaires sont distribués de manière désordonnée. |
| 554/553 | 2 | |||
| 553/552 | 3 | A | ||
| 552/551 | 4 | |||
| 551/550 | 5 | |||
| 550/549 | 6 | A | ||
| 549/548 | 7 | |||
| 548/547 | 8 | |||
| 547/546 | 9 | |||
| 546/545 | 10 | U | ||
| 545/544 | 11 | |||
| 544/543 | 12 | A | ||
| 543/542 | 13 | |||
| 542/541 | 14 | |||
| 541/540 | 15 | A | ||
| 540/539 | 16 | |||
| 539/538 | 17 | |||
| Cyrus | 538/537 | 1 | ||
| 537/536 | 2 | U | ||
| 536/535 | 3 | A | ||
| 535/534 | 4 | |||
| 534/533 | 5 | |||
| 533/532 | 6 | A | ||
| 532/531 | 7 | |||
| 531/530 | 8 | |||
| 530/529 | 9 | U | ||
| Cambyse | 529/528 | 1 | ||
| 528/527 | 2 | |||
| 527/526 | 3 | U | Trois cycles de 8 ans (octaétérides) avec trois mois complémentaires par cycle. | |
| 526/525 | 4 | |||
| 525/524 | 5 | A | ||
| 524/523 | 6 | |||
| 523/522 | 7 | |||
| 522/521 | 8 | A | ||
| Darius | 521/520 | 1 | ||
| 520/519 | 2 | |||
| 519/518 | 3 | U | ||
| 518/517 | 4 | |||
| 517/516 | 5 | A | ||
| 516/515 | 6 | |||
| 515/514 | 7 | |||
| 514/513 | 8 | A | ||
| 513/512 | 9 | |||
| 512/511 | 10 | |||
| 511/510 | 11 | U | ||
| 510/509 | 12 | |||
| 509/508 | 13 | A | ||
| 508/507 | 14 | |||
| 507/506 | 15 | |||
| 506/505 | 16 | A | ||
| 505/504 | 17 | |||
| 504/503 | 18 | |||
| 503/502 | 19 | U | Un cycle de 19 ans. Deux irrégularités : 1) Un second Addaru l'année 23 du règne au lieu de l'année 21. 2) Un second Ullulu l'année 30 du règne au lieu d'un second Addaru l'année 29 | |
| 502/501 | 20 | |||
| 501/500 | 21 | |||
| 500/499 | 22 | A | ||
| 499/498 | 23 | |||
| 498/497 | 24 | A | ||
| 497/496 | 25 | |||
| 496/495 | 26 | |||
| 495/494 | 27 | A | ||
| 494/493 | 28 | |||
| 493/492 | 29 | |||
| 492/491 | 30 | U | ||
| 491/490 | 31 | |||
| 490/489 | 32 | A | ||
| 489/488 | 33 | |||
| 488/487 | 34 | |||
| 487/486 | 35 | A | ||
| 486/485 | 36 | |||
| Xerxès | 485/484 | 1 | ||
| 484/483 | 2 | U | Un cycle de 19 ans. Une irrégularité : Un second Ullulu l'année 7 du règne au lieu d'un second Addaru. | |
| 483/482 | 3 | |||
| 482/481 | 4 | A | ||
| 481/480 | 5 | |||
| 480/479 | 6 | |||
| 479/478 | 7 | U | ||
| 478/477 | 8 | |||
| 477/476 | 9 | |||
| 476/475 | 10 | A | ||
| 475/474 | 11 | |||
| 474/473 | 12 | A | ||
| 473/472 | 13 | |||
| 472/471 | 14 | |||
| 471/470 | 15 | A | ||
| 470/469 | 16 | |||
| 469/468 | 17 | |||
| 468/467 | 18 | A | ||
| 467/466 | 19 | |||
| 466/465 | 20 | |||
| 465/464 | 21 | U | Un cycle de 19 ans. Pas de texte mentionnant un mois complémentaire l'année 8 du règne. | |
| Artaxerxès | 464/463 | 1 | ||
| 463/462 | 2 | A | ||
| 462/461 | 3 | |||
| 461/460 | 4 | |||
| 460/459 | 5 | A | ||
| 459/458 | 6 | |||
| 458/457 | 7 | |||
| 457/456 | 8 | ? | ||
| 456/455 | 9 | |||
| 455/454 | 10 | A | ||
| 454/453 | 11 | |||
| 453/452 | 12 | |||
| 452/451 | 13 | A | ||
| 451/450 | 14 | |||
| 450/449 | 15 | |||
| 449/448 | 16 | A | ||
| 448/447 | 17 | |||
| 447/446 | 18 | |||
| 446/445 | 19 | A | Un cycle de 19 ans. Une irrégularité : Un second Addaru l'année 19 du règne au lieu d'un second Ullulu. | |
| 445/444 | 20 | |||
| 444/443 | 21 | A | ||
| 443/442 | 22 | |||
| 442/441 | 23 | |||
| 441/440 | 24 | A | ||
| 440/439 | 25 | |||
| 439/438 | 26 | |||
| 438/437 | 27 | A | ||
| 437/436 | 28 | |||
| 436/435 | 29 | A | ||
| 435/434 | 30 | |||
| 434/433 | 31 | |||
| 433/432 | 32 | A | ||
| 432/431 | 33 | |||
| 431/430 | 34 | |||
| 430/429 | 35 | A | ||
| 429/428 | 36 | |||
| 428/427 | 37 | |||
| 427/426 | 38 | A | Un cycle de 19 ans. Une irrégularité : Un second Addaru l'année 19 du règne au lieu d'un second Ullulu. Même erreur que pour le cycle précédent sous le règne du même roi. | |
| 426/425 | 39 | |||
| 425/424 | 40 | A | ||
| 424/423 | 41 | |||
| Darius II | 423/422 | 1 | ||
| 422/421 | 2 | A | ||
| 421/420 | 3 | |||
| 420/419 | 4 | |||
| 419/418 | 5 | A | ||
| 418/417 | 6 | |||
| 417/416 | 7 | A | ||
| 416/415 | 8 | |||
| 415/414 | 9 | |||
| 414/413 | 10 | A | ||
| 413/412 | 11 | |||
| 412/411 | 12 | |||
| 411/410 | 13 | A | ||
| 410/409 | 14 | |||
| 409/408 | 15 | |||
| 408/407 | 16 | U | Un cycle de 19 ans. Pas d'irrégularité. | |
| 407/406 | 17 | |||
| 406/405 | 18 | A | ||
| 405/404 | 19 | |||
| Artaxerxès II | 404/403 | 1 | ||
| 403/402 | 2 | A | ||
| 402/401 | 3 | |||
| 401/400 | 4 | |||
| 400/399 | 5 | A | ||
| 399/398 | 6 | |||
| 398/397 | 7 | A | ||
| 397/396 | 8 | |||
| 396/395 | 9 | |||
| 395/394 | 10 | A | ||
| 394/393 | 11 | |||
| 393/392 | 12 | |||
| 392/391 | 13 | A | ||
| 391/390 | 14 | |||
| 390/389 | 15 | |||
| 389/388 | 16 | U | Un cycle de 19 ans. Une irrégularité : Un second Addaru l'année 20 du règne aurait dû être intercalé l'année suivante. | |
| 388/387 | 17 | |||
| 387/386 | 18 | A | ||
| 386/385 | 19 | |||
| 385/384 | 20 | A | ||
| 384/383 | 21 | |||
| 383/382 | 22 | |||
| 382/381 | 23 | |||
| 381/380 | 24 | A | ||
| 380/379 | 25 | |||
| 379/378 | 26 | A | ||
| 378/377 | 27 | |||
| 377/376 | 28 | |||
| 376/375 | 29 | A | ||
| 375/374 | 30 | |||
| 374/373 | 31 | |||
| 373/372 | 32 | A | ||
| 372/371 | 33 | |||
| 371/370 | 34 | |||
| 370/369 | 35 | U | Un cycle de 19 ans. Pas d'irrégularité. Le cycle est standardisé. | |
| 369/368 | 36 | |||
| 368/367 | 37 | A | ||
| 367/366 | 38 | |||
| 366/365 | 39 | |||
| 365/364 | 40 | A | ||
| 364/363 | 41 | |||
| 363/362 | 42 | |||
| 362/361 | 43 | A | ||
| 361/360 | 44 | |||
| 360/359 | 45 | A | ||
| 359/358 | 46 | |||
| Artaxerxès III | 358/357 | 1 | ||
| 357/356 | 2 | A | ||
| 356/355 | 3 | |||
| 355/354 | 4 | |||
| 354/353 | 5 | A | ||
| 353/352 | 6 | |||
| 352/351 | 7 |
À l'analyse, on peut distinguer quatre périodes distinctes :
- Avant 527/526 av. J.-C. le calendrier est bien luni-solaire mais les mois intercalaires semblent insérés au hasard. Il est difficile de croire que le cycle de 19 ans ait été connu dès Nabonassar.
- De 527/526 à 503/502 av. J.-C. plusieurs cycles de 8 ans sont appliqués avec 4 intercalations par cycle aux années 1, 3, 6. C'est l'octaétéride qui, chez les Grecs, sera découvert en 500 av. J.-C. par Cléostrate de Ténédos qui positionnera les années embolismiques en 2ème, 5 ème et 8 ème position dans le cycle. On constate aussi que le début du cycle est toujours caractérisé par une année embolismique dont le mois doublé est Ullulu alors que le mois doublé des autres années embolismiques est Addaru.
- De 503/502 à 370/369 av. J.-C. le cycle de 19 ans est appliqué avec quelques irrégularités de position et de nom de mois doublé mais sans déroger au principe de 7 intercalations dans les 19 ans. Le seul mois doublé manquant est celui de 457/456. Mais faut-il en conclure à l'absence de mois complémentaire cette année là parce qu'aucun texte n'a été retrouvé ?
- A partir de 359/358 av. J.-C. le cycle est stabilisé. Contrairement à ce qu'on peut lire ici ou là, il semble bien que le cycle commence par une année embolismique avec deux mois Ullulu dans la continuité de ce qui avait été fait pour les cycles de 8 ans. Partant de ce principe que le cycle commence par une année avec un double Ullulu, les intercalations se seraient faites les 1, 3, 6, 9, 11, 14, et 17 ème années.
En guise de conclusion
Méton a-t-il inventé le cycle qui porte son nom ?
Il semble bien que non puisque les Babyloniens et les Chinois l'avaient précédé.
Mais, après tout, il n'avait pas demandé à ce que ce cycle de 19 ans porte son nom !! Et rien ne prouve qu'il connaissait l'existence des autres.









