- Accueil
- À ne pas manquer
- Calendriers Saga
- Les calendriers
- Le calendrier maya
Un peu d'histoire
Ce qu'on appelle quelquefois -à tort- l'empire Maya appartient à cette « Amérique moyenne » nommée Mésoamérique (ou Méso-Amérique) par l'ethno-historien Paul Kirchhoff. La Méso-Amérique se caractérise par les similitudes d'un ensemble de traits culturels, répartis sur un vaste territoire. Ce territoire correspond, en gros, au centre et au sud du Mexique et à une grande partie de l'Amérique centrale, jusqu'au sud du Costa Rica. Une acception reconsidérée y a intégré, depuis, le Panama, une frange septentrionale (jusqu'à la frontière des États-Unis), et divers éléments caraïbes de la « Méditerranée américaine », îles et littoral de la Floride aux Guyanes. (Source Encyclopædia Universalis ).
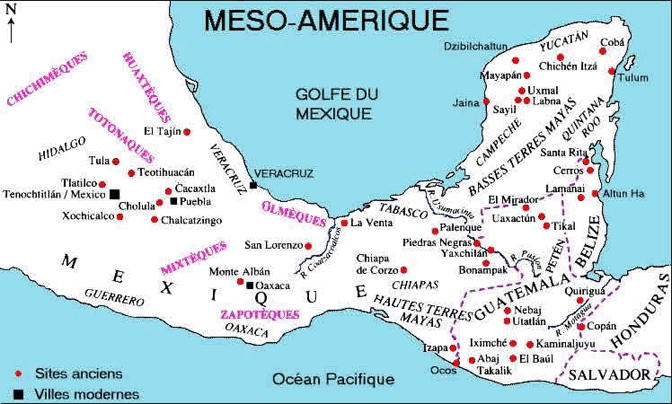
Les différentes civilisations qui occupèrent cette partie du monde furent les suivantes :
- Olmèques (-1200 à -400) : Civilisation mère qui occupa les bords du Golfe du Campeche.
- Zapotèques (-800 à -500) : Successeurs des Olmèques .
- Teotihuacan (300 à 750) : Civilisation qui vivait dans la ville du même nom .
- Toltèques (1000 à 1150) : Venus du Nord.
- Chichimèques : Groupe de tribus semi-civilisées au Nord et dont les Aztèques prirent les terres.
- Tarasques : Tribu qui résista à l'invasion aztèque menée par Axayacatl Tlaxcaliens/Tlaxcalans Tribu qui s'allia aux Espagnols contre les Aztèques.
- Totonaques : Autre tribu qui s'est alliée aux Espagnols
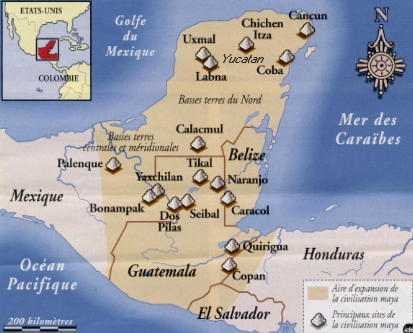
La région maya correspond à la presqu'île du Yucatan, au Guatemala, à Belize et à une partie des états actuels du Salvador et du Honduras. La civilisation maya est apparue dès -1600. Ils descendraient des Olmèques, mais ils furent malgré tout contemporains et commercèrent ensemble. Leur apogée s'est étendue de 250 à 700. Contrairement à presque toutes les autres civilisations précolombiennes, ils développèrent un système d'écriture. Celui-ci, très complexe, permit, une fois déchiffré, de comprendre un peu mieux les dynasties et les grandes périodes de la civilisation maya.
Les Toltèques, venus du Nord, s'installèrent au nord de la ville actuelle de Mexico. Sous la domination de Tezcatlipoca, l'empire Toltèque domina tout le Mexique central et influença les Mayas.
Les Aztèques, eux, se sont établis dans le sud du Mexique actuel vers 1200 apr. J.C. En 1345, ils fondent la ville de Mexico. Ils possèdent aussi une écriture.

Astronomie et mathématiques
Les Mayas eurent, en astronomie, une idée très précise du mouvement du Soleil, de la Terre et d'autres planètes. Ils estimèrent l'année solaire à 365,242 000 jours, chiffre très proche de celui de l'année tropique. Ils obtenaient la même précision en ce qui concerne une lunaison qu'ils estimaient à 29,53086 jours pour une lunaison moyenne.
Intéressons nous un instant à la manière dont comptaient les Mayas ce qui nous permettra de mieux comprendre leur calendrier. Comme les autres peuples d'Amérique centrale précolombienne, les Mayas utilisaient une numérotation vigésimale - base 20 et non 10 comme nous : vingtaines et puissances de vingt. La raison en est qu'ils comptaient sur leurs dix doigts... puis sur leurs dix orteils. C'est du moins ce qui se dit ! Jusqu'à 10 compris les nombres avaient un nom : de 12 à 19, le 10 servait de base (10 = lahun ; 13 = ox-lahun (3+10) ; 14 = can-lahun (4+10), etc). Le 11 fait exception pour éviter une confusion avec « une dizaine ». Pour les particularités de cette numérotation vigésimale, voir la note en bas de page après avoir lu l'ensemble de la page pour mieux comprendre.
Notons aussi que les Mayas avaient inventé le zéro alors que l'occident a dû attendre le moyen âge pour en « hériter » des Arabes qui le tenaient eux-mêmes des savants de l'Inde.
Le(s) calendrier(s)
Les Mayas utilisaient en fait deux calendriers :
- Le premier est le calendrier Tzolkin (cycle divinatoire) d'un usage essentiellement religieux. Il est aussi appelé « almanach sacré », « calendrier magique » ou « calendrier rituel ».
- Le second est le calendrier Haab d'un usage agricole. Il est aussi appelé « calendrier séculier », « calendrier civil » ou « calendrier vague ».
Pour être complet dans notre étude, il nous faudra ajouter :
- Le cycle sacré des 52 ans nommé Calendar Round (compte calendaire) ou, en français, « Cycle de calendrier » qui combine les deux calendriers précédents.
- Le cycle long ou compte long qui, un peu comme le système julien, permettait de compter les jours de façon linéaire par rapport à une « date zéro ». Ces jours pouvaient être comptés jusqu'à...23 milliards d'années.
1) Le Calendrier Tzolkin
L'année religieuse des Mayas se composait de treize périodes de vingt jours et comptait donc 260 jours.
Les 20 jours étaient associés à 20 glyphes différents et étaient mis en relation avec des divinités, des animaux ou des objets sacrés.
Ces 20 jours de base étaient cycliquement affectés d'un signe numératif.
| Les jours | Les signes numeratifs | ||
|---|---|---|---|
| Glyphe | Jour | Association | |

| IMIX | Crocodile |
|

| IK | Vent |
|

| AKBAL | Maison |
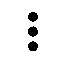
|

| KAN | Lézard |
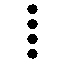
|

| CHICCHAN | Serpent |
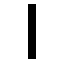
|

| CIMI | Mort |
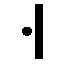
|

| MANIK | Chevreuil |
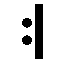
|
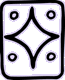
| LAMAT | Lapin |
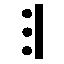
|

| MULUC | Eau |

|

| OC | Chien |
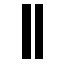
|
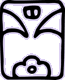
| CHUEN | Singe |
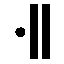
|

| EB | Herbe |
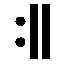
|

| BEN | Roseau |
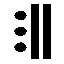
|
| IX | Jaguar | |

| MEN | Aigle | |

| CIB | Vautour | |

| CABAN | Mouvement | |

| EZNAB | Couteau de silex | |

| CAUAC | Pluie | |

| AHAU | Fleur | |
Comment étaient associés les jours et les numéros ? En déroulant les jours du calendrier et en leur affectant un nouveau numéro. Lorsqu'on arrivait au numéro 13, on enchaînait à nouveau par le numéro 1. Au bout de 260 jours, le cycle était bouclé.
La façon la plus imagée pour se représenter ce déroulement est d'imaginer deux roues d'engrenage qui tournent :
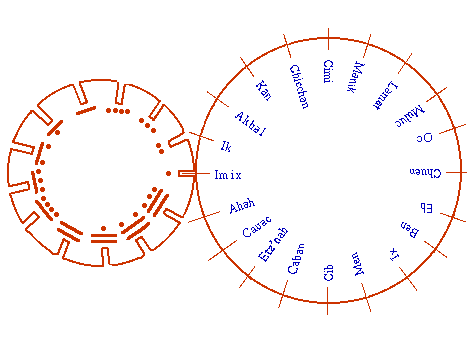



Exemples de « numérotation » des jours
Le tableau ci-dessous se lit en croisant les lignes et les colonnes. Le nombre indiqué en bleu indique la période de retour des jours. Le nombre trouvé à l'intersection est celui qui est associé au nom du jour. (1 Imix ; 2 Ik ; 3 Akbal...8 Imix ; 9 Ik...). Ainsi, Kan ne peut être associé qu'aux nombres 4, 11, 5, 12, 6, 13, 7, 1, 8, 2, 9, 3, 10.
Au passage, notons que si le choix de 20 jours peut se comprendre aisément dans une numérotation vigésimale, l'utilisation d'une base 13 pour les périodes reste un mystère.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IMIX | 1 | 8 | 2 | 9 | 3 | 10 | 4 | 11 | 5 | 12 | 6 | 13 | 7 |
| IK | 2 | 9 | 3 | 10 | 4 | 11 | 5 | 12 | 6 | 13 | 7 | 1 | 8 |
| AKBAL | 3 | 10 | 4 | 11 | 5 | 12 | 6 | 13 | 7 | 1 | 8 | 2 | 9 |
| KAN | 4 | 11 | 5 | 12 | 6 | 13 | 7 | 1 | 8 | 2 | 9 | 3 | 10 |
| CHICCHAN | 5 | 12 | 6 | 13 | 7 | 1 | 8 | 2 | 9 | 3 | 10 | 4 | 11 |
| CIMI | 6 | 13 | 7 | 1 | 8 | 2 | 9 | 3 | 10 | 4 | 11 | 5 | 12 |
| MANIK | 7 | 1 | 8 | 2 | 9 | 3 | 10 | 4 | 11 | 5 | 12 | 6 | 13 |
| LAMAT | 8 | 2 | 9 | 3 | 10 | 4 | 11 | 5 | 12 | 6 | 13 | 7 | 1 |
| MULUC | 9 | 3 | 10 | 4 | 11 | 5 | 12 | 6 | 13 | 7 | 1 | 8 | 2 |
| OC | 10 | 4 | 11 | 5 | 12 | 6 | 13 | 7 | 1 | 8 | 2 | 9 | 3 |
| CHUEN | 11 | 5 | 12 | 6 | 13 | 7 | 1 | 8 | 2 | 9 | 3 | 10 | 4 |
| EB | 12 | 6 | 13 | 7 | 1 | 8 | 2 | 9 | 3 | 10 | 4 | 11 | 5 |
| BEN | 13 | 7 | 1 | 8 | 2 | 9 | 3 | 10 | 4 | 11 | 5 | 12 | 6 |
| IX | 1 | 8 | 2 | 9 | 3 | 10 | 4 | 11 | 5 | 12 | 6 | 13 | 7 |
| MEN | 2 | 9 | 3 | 10 | 4 | 11 | 5 | 12 | 6 | 13 | 7 | 1 | 8 |
| CIB | 3 | 10 | 4 | 11 | 5 | 12 | 6 | 13 | 7 | 1 | 8 | 2 | 9 |
| CABAN | 4 | 11 | 5 | 12 | 6 | 13 | 7 | 1 | 8 | 2 | 9 | 3 | 10 |
| EZNAB | 5 | 12 | 6 | 13 | 7 | 1 | 8 | 2 | 9 | 3 | 10 | 4 | 11 |
| CAUAC | 6 | 12 | 7 | 1 | 8 | 2 | 9 | 3 | 10 | 4 | 11 | 5 | 12 |
| AHAU | 7 | 1 | 8 | 2 | 9 | 3 | 10 | 4 | 11 | 5 | 12 | 6 | 13 |
Les 260 jours du calendrier maya tzolkin
Notons que les 13 nombres étaient associés aux Oxlahuntiku, treize divinités Mayas du monde supérieur. Ils possédaient donc leur propre valeur rituelle.
2) Le Calendrier Haab
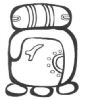
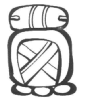
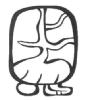
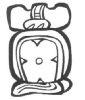
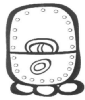
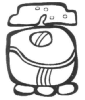
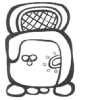
Dans ce calendrier « civil » de type solaire, l'année comportait 365 jours répartis en 18 mois (uinal) de 20 jours chacun auxquels s'ajoutait un période complémentaire de cinq jours en fin d'année. Les 18 mois étaient consacrés à des divinités et portaient le nom de manifestations religieuses ou agricoles. Le glyphe qui y était attaché représentait le dieu ou l'animal sacré symbolisant cette manifestation.
Quant à la période des 5 jours additionnels, elle était désignée par le terme de Uayeb qui signifiait « Celui qui n'a pas de nom » et était réputée être une période de malchance.
Tous les jours étaient numérotés de 0 à 19 mais le premier (notre zéro) était appelé « fin du mois » ou « début du mois suivant » et son glyphe était accompagné d'un glyphe « zéro ». Les autres jours de chaque période « mensuelle » étaient numérotés de 1 à 19. Ainsi 5 Mol était en fait le sixième jour du mois de « Mol ».
| 1 |

| POP | 11 |
| ZAC |
| 2 |
| UO | 12 |
| CEH |
| 3 |
| ZIP | 13 |

| MAC |
| 4 |

| ZOTZ | 14 |
| KANKIN |
| 5 |

| TZEC | 15 |

| MUAN |
| 6 |

| XUL | 16 |

| PAX |
| 7 |
| YAXKIN | 17 |

| KAYAB |
| 8 |
| MOL | 18 |
| CUMKU |
| 9 |
| CHEN | UAYEB |

| UAYEB |
| 10 |

| YAX |
Glyphes et noms des 18 uinal + période de 5 jours
Dans ce calendrier, chacun des 20 jours de la série Imix, Ik, Akbal... Ahau se retrouvait à la même place dans chacun des 18 uinal d'une même année. Un peu comme si, par exemple, le mardi de l'année 2002 se trouvait toujours le 5 de chaque mois.
Mais, comme il y avait 5 jours additionnels, chaque jour changeait de numéro chaque année par rapport à l'année précédente. Chaque année, les 20 jours étaient décalés par série de 5. Ce n'est donc qu'au bout de 5 ans que les noms retrouvaient leur numéro de départ. De ce fait, quatre jours seulement pouvaient se trouver en tête d'année et constituer le « nouvel an » : Eb, Caban, Ik, Manik.
3) Le Compte calendaire
Les Mayas utilisaient simultanément les deux calendriers et une date complète comportait à la fois celle du calendrier « civil » et celle du calendrier « rituel ». Ainsi, une date complète était, par exemple, « 13 AHAU 18 CUMKU ». Ce jour « double » ne se retrouvait qu'au bout de 18 980 jours soit 52 années « vagues » (ou 73 années Tzolkin).
4) Le Compte long
Pas plus que le compte calendaire, le compte long ne peut être considéré comme un calendrier. Il s'agit, en effet, de dater les jours à partir d'une origine et de façon linéaire.
Le système comprenait plusieurs « unités périodiques » que les mayas « entassaient » (voir note en bas de page) pour marquer la date voulue. Chacune des périodes était associée à une représentation spéciale qui pouvait revêtir différentes formes comme tous les glyphes que nous avons déjà vus.
Voyons une de ces représentations qui va nous permettre de comprendre les différentes unités de ce système de comput :
| Ordre d'unites | Glyphe | Noms | Équivalence | Nbre de jours |
|---|---|---|---|---|
| 1 |

| Kin Jour | 0 | 1 |
| 2 |

| Uinal Mois de 20 jours | 20 kin | 20 |
| 3 |

| Tun "année de 18 mois" | 18 uinal | 360 |
| 4 |
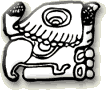
| Katun Cycle de 20 "ans" | 20 tun | 7 200 |
| 5 |

| Baktun Cycle de 400 "ans" | 20 katun | 144 000 |
| 6 |

| Pictun Cycle de 8 000"ans" | 20 baktun | 2 880 000 |
| 7 |

| Calabtun Cycle de 160 000 "ans" | 20 pictun | 57 600 000 |
| 8 |

| Kinchiltun Cycle de 3 200 000 "ans" | 20 calabtun | 1 152 000 000 |
| 9 |

| Alautun Cycle de 640 000 000 "ans" | 20 kinchiltun | 23 040 000 000 |
Quelle était l'origine de ce comput ? Ce compte long avait pour origine la date nommée 13 baktun, 4 ahau, 8 cumku correspondant au 12 août 3114 av. J.C de notre calendrier grégorien (12 août -3113). C'est du moins une des dates possibles (voir l'étude sur les ères et cycles pour les différentes hypothèses dont les plus retenues actuellement sont 11, 12 ou 13 août 3114 av. J.-C.).
Cette date se décompose comme suit : compte long : 0.0.0.0.0 ; calendrier Tzolkin : 4 Ahau ; calendrier Haab : 8 Cumku. Elle est aussi quelquefois notée 13.0.0.0.0 au lieu de 0.0.0.0.0 signifiant certainement ainsi la fin d'un cycle précédent. Le cycle actuel se terminera lorsqu'il sera arrivé à nouveau à 13.0.0.0.0 soit en 2012. Selon certaines hypothèses, la date 0.0.0.0.0 correspondrait, pour les Mayas, à la date de création du monde ou celle de la naissance de certaines de leurs divinités.
Au travers d'un exemple, celui de la Plaque de Leyde, nous allons mettre en Oeuvre le système de datation du compte long.


La plaque de Leyde à été découverte en 1864 à Puerto Barrios (Guatemala), hors contexte archéologique.
Elle aurait été gravée à Tikal.
Plate, de forme rectangulaire aux angles arrondis, haute de 21,7 centimètres, en jade vert clair finement poli, gravée sur ses deux faces à la manière d’une stèle maya miniature, la ‘plaque’ conservée à Leyde (Rijksmuseum voor Volkenkunde) est en fait une somptueuse sonnaille, un ornement qui s’accrochait en grappe aux masques de ceinture des souverains mayas, à la manière de celles que porte le personnage représenté au recto de la plaque de Leyde.
Sur sa partie face, on peut voir un personnage Maya richement vêtu piétinant un prisonnier.
Au revers, on distingue une date incisée.
Les glyphes du revers de la plaque se lisent de haut en bas.
On trouve tout d'abord (1) le glyphe introducteur de la série initiale qui correspond au nom de la divinité qui patronne le « mois » de l'année civile dans lequel tombe le jour où l'inscription fut gravée : YAXKIN
Ensuite, on trouve la date en compte long :
(2) 8 baktum
(3) 14 katum
(4) 3 tun
(5) 1 uinal
(6) 12 kin
ce qui donne :
8 baktum = 8 X 144 000 j......1 152 000 j 14 katum = 14 X 7 200 j.........100 000 j 3 tun = 3 X 360 j.................1 080 j 1 uinal = 1 X 20 j...................20 j 12 kin = 12 X 1 j....................12 j soit......................... 1 253 912 j qui correspond à l'an 320 de notre ère
Pour tout dire, les glyphes du compte long étaient le plus souvent accompagnés d'une kyrielle d'autres glyphes qui constituaient presque autant de cycles associés. Pour ne pas surcharger cette page, je vous invite, si vous voulez en savoir plus, à consulter l'annexe consacrée à ces cycles au travers de l'étude d'un linteau en pierre de Yaxchilan.
Note sur la numérotation vigésimale
La seule trace qui existe du système de numérotation maya se rapporte à l'astronomie et au comput du temps.
Comme nous l'avons vu plus haut, cette numérotation était vigésimale. Ajoutons aussi qu'elle était positionnelle. Un peu comme la nôtre, à la différence près que la nôtre positionne l'ordre des unités de droite à gauche (... centaines, dizaines, unités) alors que les Mayas les positionnaient verticalement en plaçant les unités en bas.
Par exemple, 89 (8 * 10 + 9 pour nous), s'écrivait :
| 4 x 20 |
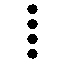
|
| 9 |

|
De même que l'ordre de rang supérieur au rang précédent est pour nous un multiple de 10 (11 450 = 1*10*10*10*10 + 1*10*10*10 + 4*10*10 + 5*10 + 0) ou [1; 1; 4; 5; 0] ce qui nous donne une progression de type 0, 10, 100, 1000, 10 000, il aurait dû être dans le système maya un multiple de 20. Nous aurions eu une progression de type 0, 20, 400, 8 000, 16 000 et notre chiffre 11 450 se serait écrit 1*20*20*20 + 8*20*20 + 12*20 + 10 ou [1; 8; 12; 10].
Or, nous avons vu plus haut, dans le compte long, que les différentes unités du comput étaient 0, 20, 360, 7 200, 144 000. 360 au lieu de 400. La numérotation vigésimale pure est interrompue au troisième rang pour, ensuite reprendre régulièrement (7 200 = 360 * 20 ; 144 000 = 7 200 * 20 ; etc.)
Et, du coup, notre chiffre 11 450 va s'écrire 1*360*20 + 11*360 + 14*20 + 10 ou [1; 11; 14; 10]. Quant à 400, qui aurait dû être sous la forme 1*20*20 + 0 ou [1; 0; 0], il devint 1*360 + 2*20 + 0 ou [1; 2; 0].
Le système vigésimal maya était donc presque vigésimal. Alors, ne croyons pas ce qui peut être dit à droite ou à gauche. Je pense particulièrement à ce qu'on peut lire dans les cahiers de Science et Vie de décembre 2003 qui s'appliquent à nous parler d'une numérotation de 20 en 20.
Mais pourquoi 360 au lieu de 400 ? Une explication serait peut-être liée à la durée de l'année. À défaut d'une autre, il nous faudra bien nous en contenter.
Cette particularité va avoir une importante conséquence : le zéro des Mayas n'a plus de possibilité opératoire. En effet, l'adjonction d'un zéro à un nombre dans une numérotation vigésimale pure aurait eu pour résultat de multiplier par la base 20 la valeur de ce nombre. Ainsi [1; 0; 0] en base 20, correspond au carré de [1; 0]. Du fait de cette « rupture » du 360 dans le système, le zéro n'a plus qu'une valeur de « remplissage » au lieu d'une possibilité opératoire.
Le zéro des Mayas n'a donc pas la même signification que notre zéro actuel.








